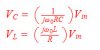resonance

[PG1995]

Thanks a lot, Ratch!

Your attempt to derive the resonant frequency with resistance present in the coil tells me that you do not quite understand the principle of parallel resonance (PR).

I agree with you that I have forgotten much of the details but at the same time I was approaching the problem differently. Please have a look here. I was thinking that "initial expression" and "final expression" are equivalent; it's just that "initial expression" has been written in terms of Q_L and later it was expanded and simplified into "final expression". In other words, I wasn't really trying to derive resonant frequency; I was more of focused on trying to derive the "final expression" using "initial expression". But it looks like they aren't equivalent.

Best,
PG

 

[Ratchit]

Thanks a lot, Ratch!



I agree with you that I have forgotten much of the details but at the same time I was approaching the problem differently. Please have a look here. I was thinking that "initial expression" and "final expression" are equivalent; it's just that "initial expression" has been written in terms of Q_L and later it was expanded and simplified into "final expression". In other words, I wasn't really trying to derive resonant frequency; I was more of focused on trying to derive the "final expression" using "initial expression". But it looks like they aren't equivalent.

Best,
PG

Assume that the capacitor branch also contains a resistance. Can you analyze the circuit and find the relationship of L,C, Rc, and Rl where the circuit is resonant at all frequencies? What would the impedance be across the two parallel branches?

Ratch

 

[MrAl]

Hi,

Could you please help me with the question below?

Please have a look on the attachment. I'm not sure how they are getting to this final expression. I had thought that perhaps they started with the 'initial expression' and after simplification got this final expression but it looks like I was wrong. You can see below that I tried to simplifyy the initial expression but it ended up to something different from final expression. Thank you!

Note to self:
Q (the “quality factor”), is a measure of how much energy is not lost in a reactive element. The higher the Q, the less energy is lost. Quality factor exist for inductor as well as capacitor. Q_C=Xc/Rc=1/(2*pi*f*C*Rc) and Q_L=X_L/R_w=2*pi*f*L/Rw where Xc=1/(2*pi*f*C) is capacitive reactance, Rc is equivalent series capacitor resistance, X_L=2*pi*f*L and Rw is equivalent series winding resistance. When the resistance is just the winding resistance of the coil, the circuit Q and the coil Q are the same.
Helpful link(s): https://www.capacitorguide.com/q-factor/

Hello,

The fact is they DID start with the initial expression and got the more exact result. You just did not do something right in the algebra.
You should try this again unless you want me to show you the solution. Starting with the first expression in green you should get the final result in green.
In other words, solving using Q should be the same as any other way.

 

[PG1995]

Thank you!

Assume that the capacitor branch also contains a resistance. Can you analyze the circuit and find the relationship of L,C, Rc, and Rl where the circuit is resonant at all frequencies? What would the impedance be across the two parallel branches?

You can see I tried but couldn't simplify it any further in terms of ω.

The fact is they DID start with the initial expression and got the more exact result. You just did not do something right in the algebra.
You should try this again unless you want me to show you the solution. Starting with the first expression in green you should get the final result in green.
In other words, solving using Q should be the same as any other way.

I believe you if you say so. But my attempt didn't enable me to convert initial expression into the final expression. Also I wasn't able to trace any mistake in my attempt.

 

[Ratchit]

PG1995,

Good try!

As you can see, if the coil resistance squared is less than L/C AND the capacitor resistance squared is less than L/C, the number under the square root sign is positive and represents a definite frequency. The same is true if the coil resistance squared is greater than L/C AND the capacitor resistor squared is greater than L/C.

If the coil resistance squared equals the capacitor resistance squared and both equal L/C, then omega equals the square root of 0/0, and no definite frequency is obtained. Therefore, the circuit is resonant at all frequencies.

 

[PG1995]

Thanks a lot, Ratch!

I really appreciate your help. You pointed out a really good point that resonant frequency could be adjusted through resistances along with other points.

After your last post I realized that I could get quadratic equation in ω by rearranging the expression, but then that quadratic didn't end up like your end result. Then, I was trying to catch my mistake(s) in the derivation but couldn't. Perhaps, you can give it a look and help me. Thanks.

 

[Ratchit]

PG1995,
I won't help you. I did my calculations on a computer, and it does not give the intermediate steps. It only gives the result. I am not going to waste time by tediously doing the intermediate steps to find your mistake.

Ratch

 

[Ratchit]

PG1995,

Tisk, tisk. You did not find my mistake. The formula for frequency is

Ratch

 

[PG1995]

PG1995,
I won't help you. I did my calculations on a computer, and it does not give the intermediate steps. It only gives the result. I am not going to waste time by tediously doing the intermediate steps to find your mistake.

Thank you. No worries. I understand that it takes a lot of effort and time to trace a mistake in someone else's work. You've already helped me enough with this problem.

Best,
PG

 

[MrAl]

Hello again,

Well not too bad. The main thing is to do each step with the intent that you have to simplify at the end.
Here is one way to do it...

Start with the original definitions:
eq1=1/(2*pi*sqrt(C*L))
eq2=sqrt(Q^2/(Q^2+1))
Qx=XL/R
XL=2*pi*f*L

and since w=2*pi*f define:
XLw=w*L

and so the original statement is:
f=eq1*eq2=sqrt(Q^2/(Q^2+1))/(2*pi*sqrt(C*L))

or simply:
f=sqrt(Q^2/(Q^2+1))/(2*pi*sqrt(C*L))

Now multiply by 2*pi:
2*pi*f=sqrt(Q^2/(Q^2+1))/sqrt(C*L)

so:
w=sqrt(Q^2/(Q^2+1))/sqrt(C*L)

replace Q with Qx:
w=sqrt(XL^2/(R^2*(XL^2/R^2+1)))/sqrt(C*L)

simplify:
w=XL/(sqrt(C*L)*R*sqrt(XL^2/R^2+1))

replace XL with XLw:
w=(w*L)/(sqrt(C*L)*sqrt((w^2*L^2)/R^2+1)*R)

divide both sides by w:
1=L/(sqrt(C*L)*sqrt((w^2*L^2)/R^2+1)*R)

multiply by the denominator of the right side:
sqrt(C*L)*sqrt((w^2*L^2)/R^2+1)*R=L

divide both sides by R:
sqrt(C*L)*sqrt((w^2*L^2)/R^2+1)=L/R

square both sides and divide by C*L:
(w^2*L^2)/R^2+1=L/(C*R^2)

multiply by R^2:
R^2+w^2*L^2=L/C

subtract R^2:
w^2*L^2=L/C-R^2

divide by L^2:
w^2=(L/C-R^2)/L^2

simplify:
w^2=(L-C*R^2)/(C*L^2)

divide top and bottom of right side by L:
w^2=(1-(C*R^2)/L)/(L*C)

take the square root assume only positive quantities:
w=sqrt((1-(C*R^2)/L)/(L*C))

or:
w=sqrt((1-(C*R^2)/L))/sqrt(L*C)

divide both sides by 2*pi:
f=sqrt((1-(C*R^2)/L))/(2*pi*sqrt(L*C))

and there we ended up with the final expression.

You can combine some steps of course if you like.
This is just algebra though nothing more.

 

[PG1995]

Thank you, MrAl.

It's impressive how you got the final expression. Yes, it's just algebra but one could easily make mistake(s) when simplification takes many steps.

Best,
PG

 

[PG1995]

Hi,

I have quite a few questions about some post in this thread. I just need some clarification about those questions. I'd really appreciate if you could help me.

Question 1:
In this post, post #3, Diver300 said:

Also, that is a resonant circuit with a very low Q. The resistance of the resistor is larger than the in reactances. In a circuit that actually has useful resonance, you would expect the reactances to be large compared to the resistance. A series tuned circuit like that, when at the resonant frequency, would have much more voltage across the capacitor or the inductor than across the resistor.

He was commenting on this series RLC circuit. In a series RLC circuit voltage amplification is given as:

The voltage across the capacitor or inductor is inversely proportional to the resistance. I see a contradiction in Diver300 's statement. First, he is saying that resistance is large in the given circuit and then he is saying that in such a circuit much more voltage would appear across the capacitor or inductor... At resonance voltage across resistor is just equal to Vin. So, what am I missing here?

Question 2:
In this post, post #5, MikeMl posted the following table.

I think I(V1) is the current supplied by the source. I don't understand why phase for I(V1) is -180 degrees. Shouldn't it be 0 degrees?

Question 3:
In this post, post #6, MikeMl said.

Who is to say that low Q is not more desirable with respect to ringing and/or transient response than high Q. Both low Q and high Q versions of this circuit could be "better", depending on what the goal is...?

"In electrical circuits, ringing is an unwanted oscillation of a voltage or current.Ringing is undesirable because it causes extra current to flow, thereby wasting energy and causing extra heating of the components." [Reference: https://en.wikipedia.org/wiki/Ringing_(signal)]

In a series RLC circuit current is same around the circuit and it is dictated by resistance at resonant frequency so no 'extra current' flow problem. High Q would cause a large voltage appear across capacitor and inductor. But, yes, ringing could be explained in the context of this circuit as voltage spike(s). Do I make sense?

Also, how transient response is affected by high/low Q?

Question 4:
In this post, post #6, what are those "m^0" symbols on the right side of plot? I have pointed those "m^0" here.

Question 5:
Near the end of this post, post #8, MikeMl asked me the following question.

Do you understand why at much below resonance, V(z) approaches 5V, and much above resonance, it approaches 0V?

V(z) is across capacitor. At low frequencies a capacitor has high reactance but as the frequency increases, its reactance starts decreasing. So, at low frequencies more voltage would appear across the capacitor and at high frequencies low voltage. Correct?

Question 6:
In this post, post #5, MikeMl used a plot with dB scale.

Please have a look here.

Solid lines represent voltages.

The dotted lines represent the phases.

1 KHz is resonant frequency and all the voltage appear acoss the resistor, V(x) and phase is 0 degrees. I have marked the voltage V(s), blue mark, and its phase with blue mark circled red. This voltage is 5V.

At resonant frequency V(y) should be 0 V and you can see that it extends toward negative dB scale and this is correct.

V(z) is voltage across the capacitor. At resonant frequency it should be 3.3333 V.

I don't understand how V(x) and V(z) are almost equal low frequencies; for example, look around 100 Hz and above it.

Thank you very much!

 

[Diver300]

Hi,

I have quite a few questions about some post in this thread. I just need some clarification about those questions. I'd really appreciate if you could help me.

Question 1:
In this post, post #3, Diver300 said:


He was commenting on this series RLC circuit. In a series RLC circuit voltage amplification is given as:

The voltage across the capacitor or inductor is inversely proportional to the resistance. I see a contraction in Diver300 's statement. First, he is saying that resistance is large in the given circuit and then he is saying that in such a circuit much more voltage would appear across the capacitor or inductor... At resonance voltage across resistor is just equal to Vin. So, what am I missing here?

What I was saying was that in the given circuit, the resistance is large compared to the inductor or capacitor impedances. That makes the Q-factor low, and so the resonance peak is spread out over a wide frequency range, and the voltage across the inductor or capacitor is always small compared to the voltage across the resistor.

By contrast, a circuit with a higher Q-factor has the resistance small compared to the inductor or capacitor impedances. That would make the resonance peak much narrower, and it is in a high Q-factor circuit that there is more voltage across the inductor and capacitor, not in the low Q-factor circuit in the example. I don't think that I made that clear originally.

You are correct in saying that at resonance the voltage across the resistor is Vin. That is true no matter what the Q-factor is. If there is a high Q-factor the voltage across the inductor and capacitor will be larger than Vin, and the Q-factor is a measure of how big the voltages across the inductor and capacitor become.

The circuit in the example would not show much change in behaviour away from resonance. At half or twice the frequency, the impedance would increase to 2.12 kOhms, from 1.5 kOhms at resonance. As a teaching example, that doesn't make any difference.

Edit:-
In the first post, this was said:-

For a series RLC circuit, it is said that at resonance frequency, the individual voltage across capacitor and inductor is equal and larger than the source voltage but 180 degrees out of phase with each which results into net voltage across capacitor and inductor to be zero.

That is generally true, but in the example, the resonance is so weak that, at resonance, the voltages across the capacitor and inductor are still smaller than the source voltage.

In a series resonant circuit, at resonance, the voltage across the resistor is equal to the source voltage, and that is the largest it can be. The voltages across the capacitor and the inductor cancel out by being equal and 180 degrees out of phase. However, it's not correct that the voltages across the inductor and capacitor will always be larger than the source voltage. That depend on the Q-factor of the circuit. A heavily-damped circuit like the example has a low Q-factor and a low voltage across the inductor and capacitor.

 

[MrAl]

Thank you, MrAl.

It's impressive how you got the final expression. Yes, it's just algebra but one could easily make mistake(s) when simplification takes many steps.

Best,
PG

Hi again PG,

Oh thanks but it just did it the way it came natural to me. One little step at a time and we eventually get there.
Most of us these days use automated software for the intermediate steps so there is almost no chance of a mistake. For example, we we have na expression:
k+3*x=-12*k+3*x+1

we can look at it and see that it should help to subtract 3*x from both sides so we just type:
%-3*x

and the result spits out:
k=1-12*k

and then we go from there. if you dont want intermediate steps sometimes you can just solve it, but sometimes the software will come up with a solution that is too complicated so you have to do a little work yourself like subtract the 3*x first.

 

[PG1995]

Thank you, Diver300 , for helping with Question 1.

My other questions were about MikeMl 's posts and it looks like he might not be active these days so could someone else please chip in? I need to get over it. Thanks.

 

[PG1995]

Hi,

Could someone please comment on my Question 2 to Question 6 from post #52? Thank you.

 

[Diver300]

Question 3:
In this post, post #6, MikeMl said.


"In electrical circuits, ringing is an unwanted oscillation of a voltage or current.Ringing is undesirable because it causes extra current to flow, thereby wasting energy and causing extra heating of the components." [Reference: https://en.wikipedia.org/wiki/Ringing_(signal)]

In a series RLC circuit current is same around the circuit and it is dictated by resistance at resonant frequency so no 'extra current' flow problem. High Q would cause a large voltage appear across capacitor and inductor. But, yes, ringing could be explained in the context of this circuit as voltage spike(s). Do I make sense?

Also, how transient response is affected by high/low Q?

The quote from Wikipedia doesn't refer to a specific circuits. There are many situations where impedance from the resistance is expected to be small compared to the other impedances, so if resonance causes the other impedances to cancel out, the circuit is simply not designed to work like that.

As an example, I built a circuit with an unexpected and undesirable series resonance. A 240 V, 50 Hz relay coil was controlled by a thermostat. There were switching spikes causing interference, so I added a contact suppressor in parallel with the contacts, something like this.

I had inadvertently made a tuned circuit with the contact suppressor's capacitance and the inductance of the relay. With the relay open, the inductance was too small to resonate, so there were no problems, and the small leakage current of the suppressor didn't affect the relay.

However, when the thermostat turned on, the relay operated, and it's inductance increased. That didn't make a tuned circuit as the suppressor was shorted by the thermostat. When the thermostat turned off again, the relay coil's inductance resonated with the suppressor and more current flowed than when the thermostat was turned on. The voltage across the relay and the voltage across the suppressor were both considerably more than the 240 V supply voltage, and the relay stayed turned on.

The relay was designed to have its current limited by the inductance, not its resistance. When the relay is open, its inductance is small, so it takes more power, which is normal, but only lasts for a short time, so doesn't overheat the relay.

The contact suppressor is designed for the resistor to handle the current the flows when 240 V 50 Hz is applied and the current is limited by the capacitor. When surges occour, there is much bigger power dissipated in the resistor, but also only for a really short time.

Both of these components were therefore dissipating more power long term than was expected or designed for. Wikipedia is referring to situations like that.

 

[MrAl]

Hi,

Could someone please comment on my Question 2 to Question 6 from post #52? Thank you.

For question 3, "How does circuit Q affect transient response".

Well recall that a circuit that oscillates and has zero resistance oscillates forever without any additional energy (theory). So with a small resistance it will eventually damp out although it could take some time. So the higher the Q, the longer the ringing period.

For question 2, the phase looks like it should be 0 degrees but we have to know where it is measured from. Normally the reference phase is the voltage phase, and the current phase is therefore relative to that. That should make it 0 degrees because the reactive parts cancel leaving resistive only that leaves us with no phase shift.

 

[PG1995]

Hi,

I'm sorry to get back to this thread after a long period of time but I was occupied with so many other things.

As an example, I built a circuit with an unexpected and undesirable series resonance. A 240 V, 50 Hz relay coil was controlled by a thermostat. There were switching spikes causing interference, so I added a contact suppressor in parallel with the contacts

I have been trying to figure it out where you connected the contact suppressor. Did you connect the contact suppressor across A and B?

The relay was designed to have its current limited by the inductance, not its resistance. When the relay is open, its inductance is small, so it takes more power, which is normal, but only lasts for a short time, so doesn't overheat the relay.

Could you please elaborate a bit?

Thanks a lot.

 

[Diver300]

I have been trying to figure it out where you connected the contact suppressor. Did you connect the contact suppressor across A and B?

I had connected the contact suppressor between R and W.
When the contacts were open, the capacitance of the suppressor and the inductance of the coil formed a resonant circuit, allowing sufficient current to flow to keep the relay energised.

When I realised what was going on, I move the contact suppressor to between A and B. That formed a parallel circuit. When the contacts were open, there was no path for current to get to the relay, so it would only remain energised for a fraction of a second while the parallel circuit decayed to nothing.