Hi
Please use this
attachment and please help me. Thank you.
An op-amp tries to make differential voltage across its input terminals zero which also means that no input current flows into the op-amp.
In this case of Figure 12-22, it's easier to understand what is really happening. As Vout = (-Rf/Ri)Vin, therefore when value of Ri is low, the Vout is made more negative so that 'positive charge carriers', i.e. conventional current, are pulled away from the inverting input terminal of the op-amp with greater force and no charge carriers enter into the op-amp.
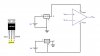
Q: The circuit on the left uses inverting configuration whose gain is given as Vout/Vin = -Rf/Ri.
In the given case Vin is negative therefore Vout = (Rf/Ri)|Vin|.
I'm assuming that the relation for Vout given above is correct. When the resistance of photoconductive cell decreases (which in this case is Ri), the Vout increases. Conceptually, I don't get why an op-amp would increase its Vout as Ri decreases.
Likewise, when Ri increases, Vout will be decreased. Why?
Regards
PG
Hi,
First, the input current is not zero. Also, if the input current is very low it is not because the differential voltage goes to zero, although that may help. The input current is dependent on the "bias" current of the particular op amp which can be found on the data sheet and usually varies with temperature. The input current is 'taken' to be zero for simplified theoretical problems like this although it is good to know the real reason why there is any input current, even though it is low.
Remember that although the differential voltage is zero or close to that, the absolute voltage on both input terminals is not always zero but some offset value or some actual DC level set by the circuit. IF the non inverting terminal is at ground, then the inverting input will be 'close' to zero but not actually zero. If it was really zero there would be no output because the differential output amplifies that small difference and that is how we get any output at all.
Also, if both inputs were zero they could be drawing current OUT of the op amp terminals, which means there is negative input current.
If you short the two inputs you'd get zero output on an ideal op amp, but a real op amp may output some voltage because of the input offset of the op amp chip.
The simplified gain can be calculated by knowing that the output feeds the feedback resistor and the input resistor 'shunts' of of that current into the input voltage source. The output will attempt to make the inverting terminal equal to the non inverting terminal in the simplified view, so we reach equilibrium when the output voltage forces the inverting terminal to the same voltage as the non inverting terminal, and to do that we have to look at the voltage divider action of the two resistors viewing the feedback resistor as the upper resistor of the divider and the input resistor as the lower resistor.
Doing that, the voltage across the two resistors is:
Vx=Vout-Vin
which as you can see could not be simpler.
The voltage at the junction referenced to Vin (not to ground) is therefore:
Vj=Vx*Rin/(Rin+Rfb)
and the voltage at the inverting terminal is that voltage with a Vin offset so we have:
Vinv=Vj+Vin
Combining all these, we get:
Vinv=(Vout-Vin)*Rin/(Rin+Rfb)+Vin
which simplifies to:
Vinv=(Rin*Vout+Rfb*Vin)/(Rin+Rfb)
Now we can just solve that for Vout and we get:
Vout=((Rin+Rfb)*Vinv-Rfb*Vin)/Rin
and if we assume that we have the simplified op amp we set Vinv=0 so we get:
Vout=-Vin*Rfb/Rin
and divding both sides by Vin we get:
Vout/Vin=-Rfb/Rin
so we see the gain is negative.
Note that Vout is not the absolute value of Vin times the 'gain', it is exactly as above.
Another view is the 'current flow' view, where the current is said to flow around the op amp. That works out the same really, and we calculate the output voltage as that which appears across the feedback resistor.
To understand the op amp a little better requires using the non ideal gain to be high but not infinite. Say 1000 would be a good plece to start. Then you can write equations based on just a plain old amplifier that amplifies the difference between the two input terminals. If we had an internal gain of 1000 for example and we had a difference voltage of 0.01 volt, we'd get 0.01 times 1000 which equals 10 volts on the output. With a difference voltage of 0.001 volt we'd get 0.001 times 1000 which equals 1 volt on the output.
Writing the equations this way brings out the fact that the op amp difference voltage really isnt zero but depends highly on the internal gain of the op amp.
We can look at more examples if you like and that is how you get a better feel for this.