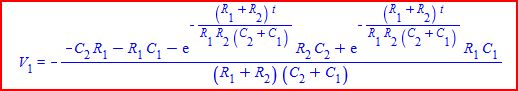Hi there Steve,
Well your argument has boiled down to what is "more useful". And that's certainly something we have to consider, but i think the scope of consideration is too small if we limit the definition to that which gives us certain solutions to certain specific problems. In this particular case where the paper is asking for a single time constant for example they want to limit us to a SINGLE one, while you yourself would be more comfortable with TWO. I believe you feel better with two because you can clearly see that one of the responses is dependent on two, not one or three or four. One of the types of responses is definitely dependent on two so it makes sense to think of these two. The two are actually easy to find if we just assume some values for the components, and we quickly see that the two constants that appear in the two exponentials are not the same for the general case.
I myself on the other hand, do not feel comfortable unless i am allowed to consider every element that can be combined into units of constant time to be a time constant. This is because i see usefulness in this view as well, and after all the units tell us they could have some relevance.
In the state equations i had shown previously i also stated that we can quickly find the slope of either voltage knowing some combinations of R and C that when multiplied come out to units of constant time. So in other words, we can find for example the slope of the voltage across C2 knowing the input step value E, the present voltage across C2, and the present voltage across C1, and also two multiplied values of R and C where the two products will be in general different from each other. Yet these values may have nothing to do with the time constants that actually determine the voltage response itself across C2 *in the analytical* solution. So that's why i see significance in thinking about other time constants too. If it were not for those two then we could not do this.
With a little thought we can even come up with the actual voltage across C2 over time without knowing anything else when we solve it numerically. During that process we would absolutely have to multiply three R's by two different values of C forming four different products of R and C. These products come out in units of constant time as constant Ohms times constant Farads equals constant Time. The units of x1 and x2 (lower case) come out to units of volts/second which is volts/time and that time is constant because all the R's and C's are constant. We would actually get the response knowing these four obscure time constants, and piecewise they actually make even more sense.
So it seems to me that you are not comfortable calling these products time constants maybe because you dont use them very often in this form, but im not sure what else to tell you. All things considered though i believe the time constants you found are time constants as well, but they have a different nature and different application that's all.
So your set is limited to only two while my set includes those two plus more

Dont get me wrong here though, i would not dare to apply them all in the same way.
This reminds me of the debate over what is a resonance and what is not. Some wish to restrict that definition to physical resonance alone while others have a more relaxed view.