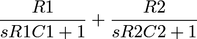No, it is one time constant for each storage element that happens to have the same value for both. Since the circuit has a symetrical topological layout, introducing a third voltage source resistance will change the value of the TC's for both, but they should still have the same values. Why would there be three TC's when there are only two storage elements?
OK, quite right that there should not be three time constants. I'm glad we agree on that point. So, for the case of nonzero source resistance Rs, we both agree that there are two time constants.
Now, you are saying that the two time constants are equal and one is assigned to one capacitor and the other is assigned to the other capacitor. My position is that this does not hold up in analysis. Above, I showed that there are two different values for the time constants, as follows, where I'm assuming the R1=R2=R and the C1=C2=C, with source resistance Rs.
T1=R C and T2=R C Rs /(2R+Rs)
Again, these come from the pole values. Now, why are these two values important? It's because the time response for both V1(t) and V2(t), which are the capacitor voltages, will have responses with these two time constants for exponential decay terms. Let's not even look at the forced response of the system, and just look at the free response from initial voltages on the caps V1(0) and V2(0).
V1(t)=(V1(0)+V2(0)) exp(-t/T2) / 2 + (V1(0)-V2(0)) exp(-t/T1) / 2
V2(t)=(V1(0)+V2(0)) exp(-t/T2) / 2 - (V1(0)-V2(0)) exp(-t/T1) / 2
So, again I stress that time constants here are associated with the circuit responses to the state variables, which I've chosen to be V1 and V2, although you could define different state variable is you wanted. If you want to assign time constants to the capacitors, presumably because these voltages are the capacitor voltages, then you need to assign both time constants to both capacitors, and the two time constants are different values, not the same values as you stated. So by your logic, it's not 2 or 3 time constants, but now it's 4 because we assign 2 values to 2 capacitors. Sorry, but it just doesn't work the way you explained it.