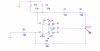
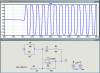
i have done a simulation of a wein bridge oscillator (without amplitude control)
from the simulation, i noticed that the output voltage(pk-pk) of the wave is approx. 2.2V and is the sine wave is not really centered to the x axis of the graph.
My circuit and simulation results are as attached.
Considering the fact that for oscillators, any transient noise signal is able to cause oscillations,
How do i determine the value of the output amplitude signal considering that there is no input source involved? (How is 2.2Vp-p in simulation obtained?) From the simulation, it is also seen that the initial start up small oscillations start from slightly below the x axis (below 0V).Why is this so?
The power supply voltages for the op amp are +20V and -20V in symmetry. Why is the wave still not centered evenly on the x axis? Is there any theory behind this or its just a simulator related problem?
_________________________________________________________________
Besides that, it is stated in theory that if the gain on the negative feedback loop is increased higher than 3, oscillations will increase in amplitude .and if the gain is reduced to less than 3, the oscillations will diminish to nothing..
From the feedback formula Avf= Ao/(1-Ao*beta)
i calculate that
why does a negative gain increase amplitude while a postive gain reduce amplitude? shouldnt it be the other way around?
or is my approach on the concept wrong?
________________________________________________________________
In the Barkhausen criteria, a 0d phase shift is required.. I understand that the frequency selective feedback loop provides a phase shift of 0d. How about the gain feedback loop involving the 2 resistors? My lecturer says the opamp provides a phase shift of 180 and the feedback gain loop provides another 180 totalling a 360.. but some teaching material on the internet says there is no phase shift by the op amp...
Help is very much appreciated=)
from the simulation, i noticed that the output voltage(pk-pk) of the wave is approx. 2.2V and is the sine wave is not really centered to the x axis of the graph.
My circuit and simulation results are as attached.
Considering the fact that for oscillators, any transient noise signal is able to cause oscillations,
How do i determine the value of the output amplitude signal considering that there is no input source involved? (How is 2.2Vp-p in simulation obtained?) From the simulation, it is also seen that the initial start up small oscillations start from slightly below the x axis (below 0V).Why is this so?
The power supply voltages for the op amp are +20V and -20V in symmetry. Why is the wave still not centered evenly on the x axis? Is there any theory behind this or its just a simulator related problem?
_________________________________________________________________
Besides that, it is stated in theory that if the gain on the negative feedback loop is increased higher than 3, oscillations will increase in amplitude .and if the gain is reduced to less than 3, the oscillations will diminish to nothing..
From the feedback formula Avf= Ao/(1-Ao*beta)
i calculate that
- when i increase the gain to higher than 3, AVF will be a negative number
- when i increase the gain to lower than 3, AVF will be a positive number
why does a negative gain increase amplitude while a postive gain reduce amplitude? shouldnt it be the other way around?
or is my approach on the concept wrong?
________________________________________________________________
In the Barkhausen criteria, a 0d phase shift is required.. I understand that the frequency selective feedback loop provides a phase shift of 0d. How about the gain feedback loop involving the 2 resistors? My lecturer says the opamp provides a phase shift of 180 and the feedback gain loop provides another 180 totalling a 360.. but some teaching material on the internet says there is no phase shift by the op amp...
Help is very much appreciated=)