Hi, I am reading about "Maximum power transfer theorem" in the page: https://en.wikipedia.org/wiki/Maximum_power_transfer_theorem
Here is the part that I don't understand. Please help me. Thanks.
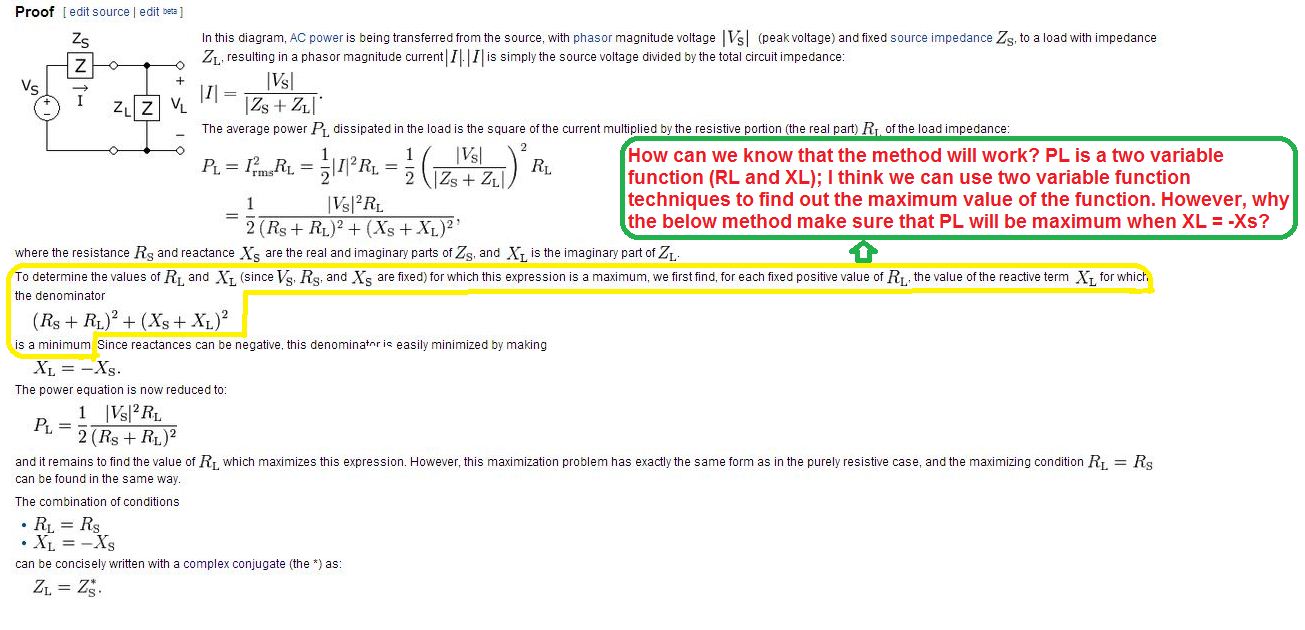
Here is the part that I don't understand. Please help me. Thanks.