Impedance for a BJT stage, with collector-base feedback resistor

[MrAl]

Hi there Ratch,


"Ask and I will answer."

Ok great...

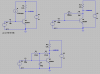
Then perhaps you would be good enough to go through a numerical example for oh say, the 2N3904 transistor. This is a common transistor for which data is available on the web. You could also state what value you intend to use for hie to calculate "RT".
I take it "RT" is what you are calling the original circuits output resistance then Rout? If not then explain how you get the value of Rout, and what numerically it comes out to in your numerical example.

 

[Ratchit]

MrAl,

Ok great...

Then perhaps you would be good enough to go through a numerical example for oh say, the 2N3904 transistor. This is a common transistor for which data is available on the web. You could also state what value you intend to use for hie to calculate "RT".
I take it "RT" is what you are calling the original circuits output resistance then Rout? If not then explain how you get the value of Rout, and what numerically it comes out to in your numerical example.

h[ie] is used to calculate Z, not R[t]. As I designated in my previous post, R[T] is the parallel combination of 1/h[oe], R[c], and R[L]. I have been ignoring h[oe] because it is so small, and R[e] because it does not exist. All your other questions should be answered in the attached file.

Ratch

 

[MrAl]

Hi again Ratch,


Yes, that's what i thought...doesnt 1020 ohms seem a little too high, like more than two times the true value? That's similar to what i was getting using your formula, so something is either missing or something else must be wrong.

 

[Jony130]

The simulation show that Rout = 280R

And I think that the main problem with Rout = 1020 ohm is the Hie value that Ratch assume.

Hie = 10K ?? ----> re = 10K/101 ≈ 100Ω---> Ic = 26mV/100Ω = 260μA ??


If I assume Hie = 2.2K (Ic = 2.28mA hfe= 200) and then use Ratch equation to find Rout

Ro = (Rg*Rf + Rf*Hie + Rg*Hie)/(Hie + Rg + Rg*Hfe) = 295.89504Ω

Rout = Ro||Rc = 277

 

[MrAl]

Hi Jony,

How did you determine that Rout was 280 ohms?
Also, how did you measure an hie value of 2.2k ?

BTW we are using a 2N3904 transistor for the example.

 

[Ratchit]

Jony and Al,

I looked at the specs for a 2N3904, and it says that hie can be between 1K and 10K. I used 10K. The hfe can be between 100 and 400, so I used 100. hoe was so small I ignored it. We should all settle on a set of numbers including R[L]. Then we can discuss what the results should be. Perhaps we should also insert some R[e] to swamp out the hie.

Ratch

 

[Jony130]

Hi Jony,
How did you determine that Rout was 280 ohms?

I build this circuit in LTspice And I use AC sweep to find Rout vs frequency



And Rout vs frequency

I change the BJT to 2N3904 and for F = 1KHz Rout = 210.718Ω

Also, how did you measure an hie value of 2.2k ?

I used this equation to find Hie

Hie ≈ re * (β +1) ≈ 26mV/Ic*(β +1)

Of course to find Hie I can also use the LTspice (Hie = 3.378KΩ).

Or we can use the this datasheet
https://www.electro-tech-online.com/custompdfs/2012/02/2N3904.pdf (page 5)

And when I use the simulation data for Hie and Hfe and use Ratch equation to find Rout

Rg = 10K; RF = 47K; Hie = 3.38K Rc = 4.7K; Hfe = 300;

Rout = Rc || (Rg*Rf + Rf*Hie + Rg*Hie)/(Hie + Rg + Rg*Hfe) = 4.7KΩ||219.9Ω = 210Ω

It seems that Ratch equation is correct.

 

[MrAl]

Hello,

What we need to do is set this up in spice like Jony did and MEASURE hie.

Just as a reminder, the output impedance is NOT the impedance with the load resistor RL connected (and RL is not Rc, Rc is the collector resistor which goes to Vcc).
For a perfect amplifier with a gain of 1 and zero output impedance, if we connect a 500 ohm resistor from the output to ground and a 1v input we get an output current of 1/500 amps.
If we connect a 500 ohm resistor in series with the output of the perfect amp, and take the output from the open end of the 500 ohm resistor, we now have an amplifier with an output impedance (resistance in this case) of 500 ohms. If we then take another 500 ohm resistor and connected it to the open end of the first and connect the other end to ground, we've now loaded that new amplifier with a 500 ohm resistor and because it already had a 500 ohm output resistance the measured output will now be exactly 0.5 volts (1v on the input again).
But the output resistance of the amp is not 500+500=1000 ohms, nor is it 500 in parallel with 500 ohms (250 ohms), the amplifier output resistance is just 500 ohms no matter what RL we connect to the output (open end of the first resistor).

I wanted to clear up just exactly what output resistance is and what it is not.

Also, what technique do you use to measure hie in a given circuit like we are looking at with the original transistor circuit?

 

[Jony130]

Also, what technique do you use to measure hie in a given circuit like we are looking at with the original transistor circuit?

Here you have the three technique that came to my mind to measure hie in this circuit
I used the first method (current source and AC analysis).

And I'm also in the team that thinks that Rc is a part of a amplifier not a load.
That is why I includes Rc in my Rout calculations.

 

[MrAl]

I build this circuit in LTspice And I use AC sweep to find Rout vs frequency

View attachment 61078

And Rout vs frequency

I change the BJT to 2N3904 and for F = 1KHz Rout = 210.718Ω


I used this equation to find Hie

Hie ≈ re * (β +1) ≈ 26mV/Ic*(β +1)

Of course to find Hie I can also use the LTspice (Hie = 3.378KΩ).

Or we can use the this datasheet
https://www.electro-tech-online.com/custompdfs/2012/02/2N3904.pdf (page 5)

And when I use the simulation data for Hie and Hfe and use Ratch equation to find Rout

Rg = 10K; RF = 47K; Hie = 3.38K Rc = 4.7K; Hfe = 300;

Rout = Rc || (Rg*Rf + Rf*Hie + Rg*Hie)/(Hie + Rg + Rg*Hfe) = 4.7KΩ||219.9Ω = 210Ω

It seems that Ratch equation is correct.

Hi Jony,

(see post just before this one)

Wow, where did you get a beta of 300 from? That's a pretty nice transistor there

Typically we were expecting an Rout of 300 to 400 ohms. The formula i had posted earlier in this thread was:

Rout=(R3*R2)/(R2+R3*B+R3)

and in terms of the new variables we had been using this comes out to:
Rout=(Rc*Rf)/(Rf+Rc*hfe+Rc)

Looking on the data sheet you linked to, i see at 1ma hfe=120, so using that:
Rout=(Rc*Rf)/(Rf+Rc*hfe+Rc)
so with Rc=4.7k, Rf=47k, hfe=120 we get:
Rout=358.8

This is close to what i measured in the circuit simulator.

Using these same parameters and hie=3600 and hfe=120 from the data sheet, i use:
RT=(Rf*Rf+Rf*hie+Rg*hie)/(hie+Rg+Rg*hfe)
and get:
1989 ohms.

This fairly high value was typical of what i was seeing and that's one of the reasons i brought up some questions about the formula for "RT".

Granted the formula i posted isnt perfect either, but it doesnt require measuring hie so it's a little easier to use too.

BTW, you dont need to do a frequency sweep as we would be happy with values at 1kHz only, no problem, since we are considering output resistance here rather than the more typical impedance which would be frequency dependent.

You should also be using an AC current source on the output not a voltage source, even though you are measuring the current.

 

[Ratchit]

MrAl,

Yes, that's what i thought...doesnt 1020 ohms seem a little too high, like more than two times the true value? That's similar to what i was getting using your formula, so something is either missing or something else must be wrong.

For the values I assumed, it is correct. Remember it is the impedance looking into the transistor without R[c]. Since R[c] is part of the impedance you want, the value of R[c] in parallel must be calculated.

Jony130,

And when I use the simulation data for Hie and Hfe and use Ratch equation to find Rout

Rg = 10K; RF = 47K; Hie = 3.38K Rc = 4.7K; Hfe = 300;

Rout = Rc || (Rg*Rf + Rf*Hie + Rg*Hie)/(Hie + Rg + Rg*Hfe) = 4.7KΩ||219.9Ω = 210Ω

It seems that Ratch equation is correct.

It should be. The General Immittance Theorem is never wrong. Also it matches what a text book says it is.

MrAl,

What we need to do is set this up in spice like Jony did and MEASURE hie.

All we have to do is agree on a value of h[ie]. I am just calculating the output impedance, not measuring h[ie]

Just as a reminder, the output impedance is NOT the impedance with the load resistor RL connected (and RL is not Rc, Rc is the collector resistor which goes to Vcc).

Certainly that is true. The General Immittance Theorem ignores the value of what is designated the load impedance.

Jony130,

And I'm also in the team that thinks that Rc is a part of a amplifier not a load.
That is why I includes Rc in my Rout calculations.

You are correct in doing so.

Jony130 & MrAl,

It appears that we get the same value if we all use the same parameters. The beta of the 2N3904 can be as high as 400 according to the data sheets. The value of 3.88k for h[ie] is well within the range specified by the data sheet, too.

Ratch

 

[MrAl]

Hello again,


Ok, i did some measuring in the circuit at the bias point and here is what i found. I'll repeat the resistance values also:

Rc=4700
Rf=47000
Rg=10000
hie=4000
hfe=180
Rout=310 ohms

and the two formulas:
Rout=(Rc*Rf)/(Rf+Rc*hfe+Rc)
RT=(Rg*Rf+Rf*hie+Rg*hie)/(hie+Rg+Rg*hfe)

and the results of using those two formulas with the measured values:

Rout=246.07
RT=384.79

So it appears that they are both within reason after all.
I had expected Rout to be a little low because i modeled the input as a voltage source rather than a voltage source in series with a resistance because that way there are less parameters to have to measure in the circuit (such as hie).

So the conclusion then is that using Rc in the equation reduces the number of measured parameters to 1, but both formulas are within a reasonable estimate range i would say.

 

[Ratchit]

MrAl,

I believe a little more clarification is in order. Why the big push on measuring the parameters of the 2N3904, when we all do not have the same transistor? The h[ie] of that transistor can vary from 1k to 10k and the beta from 100 to 400. So why can't we just agree on some parameter values and calculate the output impedance from there? I designated R[T] as the parallel combination of R[c] and R[L]=1000. In accordance with the General Immittance Theorem, when the denominator the transfer function is set to zero and and -R[t] is found, that value is the output impedance. -R[t] used in this manner for the output impedance is only a symbolic artifice, and not a real value. I perhaps should have included the value of R[c] in my node equations. Then R[t] would have only have been R[L]. Anyway, my figures say 385 ohms for the output of the transistor without R[c] in parallel. When R[c] is put in parallel, the value drops to 356 ohms. If I had included R[c] in my node equations, I would have gotten 356 ohms directly without calculating its parallel effect afterwards.

Ratch

 

[MrAl]

MrAl,

I believe a little more clarification is in order. Why the big push on measuring the parameters of the 2N3904, when we all do not have the same transistor? The h[ie] of that transistor can vary from 1k to 10k and the beta from 100 to 400. So why can't we just agree on some parameter values and calculate the output impedance from there? I designated R[T] as the parallel combination of R[c] and R[L]=1000. In accordance with the General Immittance Theorem, when the denominator the transfer function is set to zero and and -R[t] is found, that value is the output impedance. -R[t] used in this manner for the output impedance is only a symbolic artifice, and not a real value. I perhaps should have included the value of R[c] in my node equations. Then R[t] would have only have been R[L]. Anyway, my figures say 385 ohms for the output of the transistor without R[c] in parallel. When R[c] is put in parallel, the value drops to 356 ohms. If I had included R[c] in my node equations, I would have gotten 356 ohms directly without calculating its parallel effect afterwards.

Ratch

Hello Ratch,

"Why the big push on measuring the parameters of the 2N3904, when we all do not have the same transistor?"
Actually THAT is the reason why we DO have to measure parameters so this question doesnt make that much sense. If we all had the same transistor we would all have the same hie. If you want we can all use a pure linear model though, in which case a simple agreement would suffice as you say. I was using 4000 ohms for hie, and 180 for hfe because that is what i measured with the Spice model i have.

Sorry but you seem to be a bit hard to talk to when discussing these technical issues because you keep either changing your mind or you are misspeaking or something. This makes it take a lot longer to figure out what is going on.
For example, first you said that Rf did not induce negative feedback, then you changed it later to say that it actually does. Then you said you couldnt understand why Rc had to be in the equation when i presented a shortened version of an equation for Rout, now you're saying that in your own equation that you have to include Rc, when even your writeup for the equations show Rc already included in RT, which you originally stated was the output impedance. If you are going to put Rc in parallel now then you need to show a good reason for doing this (and there very well could be one i wont argue).

So you see how this can get confusing? I realize that it's not as easy to talk about these kinds of topics on the internet but the more care that goes into making a statement about fact the less time it takes to figure out what is going on, like when one equation is different than the other.

Before i sum up with the equation that has shown itself to be within 700 micro ohms of the exact output resistance, i'll back up a little to your equation which you nicely presented back in this thread in a pdf file, and show you one of the main reasons for the confusion.
If you view the attached gif file, you'll see i posted a quick snapshot of your equation and circuit. One thing you've shown here is that RT is the parallel combination of Rc and RL.
Now if we want to equate a parallel resistance Rp to two other resistors R1 and R2, we of course have:
Rp=R1*R2/(R1+R2)

In the case of RT, your pdf showed this:
RT=1/hoe||Rc||RL

and we agreed that we would ignore 1/hoe, so we are left with:
RT=Rc||RL

which of course means:
RT=Rc*RL/(Rc+RL)

Now if we solve for RL, we get:
RL=(Rc*RT)/(Rc-RT)

and here we can see that we dont get RL by putting Rc in parallel with RT.
See that now?

But if you do want to put Rc in parallel with RT anyway, then you should at least state the reason why it is valid to do such a thing and we can go from there, no problem.

Now the equation i wanted to present is this one:
Rout=(Rc*Rf*Rg+hie*Rc*Rg+hie*Rc*Rf)/(Rf*Rg+hfe*Rc*Rg+Rc*Rg+hie*Rg+hie*Rf+hie*Rc)

and that includes hie which of course has to be measured because it varies quite a bit with bias point selection.

Now this last equation computes an Rout that is within 700 micro ohms of the measured value with a perfectly linear model (like the hybrid model) and the only reason for the discrepancy is probably because of the accuracy involved in measuring the values of the voltages and currents. This uses the previously mentioned voltage source in series with a resistance as the input model rather than just the voltage source alone (which isnt too bad really i guess).

My challenge to you now is to see if you can match that equation with your own derivation

 

[Ratchit]

MrAl,

"Why the big push on measuring the parameters of the 2N3904, when we all do not have the same transistor?"
Actually THAT is the reason why we DO have to measure parameters so this question doesnt make that much sense. If we all had the same transistor we would all have the same hie. If you want we can all use a pure linear model though, in which case a simple agreement would suffice as you say. I was using 4000 ohms for hie, and 180 for hfe because that is what i measured with the Spice model i have.

The OP says in post #1 that he is trying to find the input and output impedance of a circuit using something like Pspice. That suggests a calculation, not a measurement to me. So if our calculations are to agree in value, we all have to have use the same transistor parameters.

Sorry but you seem to be a bit hard to talk to when discussing these technical issues because you keep either changing your mind or you are misspeaking or something. This makes it take a lot longer to figure out what is going on.
For example, first you said that Rf did not induce negative feedback, then you changed it later to say that it actually does.

My first contribution in this thread was post #14 where I said "R2 is not a feedback resistor for AC. It is a collector-to-base bias resistor." I further went on to suggest a method to insure that it did not function as an AC feedback resistor. Next I said in post #16 that "R2 exists for collector-to-base biasing. In post #19 I said "That is the point I am trying to make. I believe R2 should only be used for bias and not AC feedback." So my only sin on this point is that I should have said something like "R2 should not be be used as a AC feedback resistor" in the first place. So although I never said that Rf does not induce any feedback, I should have been more specific.

So you see how this can get confusing? I realize that it's not as easy to talk about these kinds of topics on the internet but the more care that goes into making a statement about fact the less time it takes to figure out what is going on, like when one equation is different than the other.

No, I don't. I believe I explained my statements sufficiently in subsequent posts.

Before i sum up with the equation that has shown itself to be within 700 micro ohms of the exact output resistance, i'll back up a little to your equation which you nicely presented back in this thread in a pdf file, and show you one of the main reasons for the confusion.
If you view the attached gif file, you'll see i posted a quick snapshot of your equation and circuit. One thing you've shown here is that RT is the parallel combination of Rc and RL.
Now if we want to equate a parallel resistance Rp to two other resistors R1 and R2, we of course have:
Rp=R1*R2/(R1+R2)

OK, so far.

In the case of RT, your pdf showed this:
RT=1/hoe||Rc||RL

and we agreed that we would ignore 1/hoe, so we are left with:
RT=Rc||RL

which of course means:
RT=Rc*RL/(Rc+RL)

Now if we solve for RL, we get:
RL=(Rc*RT)/(Rc-RT)

and here we can see that we dont get RL by putting Rc in parallel with RT.
See that now?

I think I am getting a glimpse of your confusion. First of all, I am not trying to solve for RL. RL does not figure into the output impedance. I said in post #53 "-R[t] used in this manner for the output impedance is only a symbolic artifice". I believe if you understood the General Immittance Theorem better, you would see what I was doing.

But if you do want to put Rc in parallel with RT anyway, then you should at least state the reason why it is valid to do such a thing and we can go from there, no problem.

RT contains Rc, so I am not trying to put it in parallel. I am putting the calculated value of -RT (when the denominator of the transfer function is equated to zero) in parallel with Rc to get the value of the output impedance with Rc included.

Now the equation i wanted to present is this one:
Rout=(Rc*Rf*Rg+hie*Rc*Rg+hie*Rc*Rf)/(Rf*Rg+hfe*Rc*Rg+Rc*Rg+hie*Rg+hie*Rf+hie*Rc)

and that includes hie which of course has to be measured because it varies quite a bit with bias point selection.

Now this last equation computes an Rout that is within 700 micro ohms of the measured value with a perfectly linear model (like the hybrid model) and the only reason for the discrepancy is probably because of the accuracy involved in measuring the values of the voltages and currents. This uses the previously mentioned voltage source in series with a resistance as the input model rather than just the voltage source alone (which isnt too bad really i guess).

My challenge to you now is to see if you can match that equation with your own derivation

Sure, it's easy. Notice the equation -Rt, which you included in the attachment you sent me. That is the output impedance of the transistor without Rc attached to it. The parallel result of that equation (-Rt) with Rc is exactly your equation you call Rout above. If I would have included Rc in my nodal analysis, I would have gotten the same equation as you did directly without having to do a parallel calculation.

Ratch

 

[MrAl]

Hello,


Yes, very good. But if you made it more clear in your attachment (and you still havent actually, you just refer to the theory without explanation, still, after i've told you several times) we would have reached the same equation long long ago.

QUOTE
RT contains Rc, so I am not trying to put it in parallel. I am putting the calculated value of -RT (when the denominator of the transfer function is equated to zero) in parallel with Rc to get the value of the output impedance with Rc included.
UNQUOTE

You wrote (without 1/hoe): RT=Rc||RL
and now you are saying Rout=RT||Rc when you NEVER showed that in your attachment, nor anything like that.

So explain where you got the idea to put Rc in parallel with RT, and also explain what happened to RL, and what exactly is RL then?
Also, why mention that RT=Rc||RL if you never intend to use that?

RL appears to be the load, which would mean if we knew what RT was we would calculate RL from:
RL=(Rc*RT)/(Rc-RT)

In short, you wrote one thing and meant another thing several times now, so you cant expect anything but confusion.

So you are still left to explain by what mechanism you are allowed to put Rc in parallel with RT. If you want to refer to something on the web that would be fine with me.

 

[Ratchit]

MrAl,

Yes, very good. But if you made it more clear in your attachment (and you still havent actually, you just refer to the theory without explanation, still, after i've told you several times) we would have reached the same equation long long ago.

But I did explain how to use the General Immittance Theorem in the post #40 attachment.

You wrote (without 1/hoe): RT=Rc||RL
and now you are saying Rout=RT||Rc when you NEVER showed that in your attachment, nor anything like that.

Yes, I did define R[T]=R[c]||R[L], ignoring h[oe]. And I am saying that Rout, the output impedance, is -R[T]||R[c], where -R[T] comes from the denominator of the transfer function when the denominator is set to zero. I am NOT saying that the output impedance is R[T]||R[c].

So explain where you got the idea to put Rc in parallel with RT, and also explain what happened to RL, and what exactly is RL then?
Also, why mention that RT=Rc||RL if you never intend to use that?

I am not putting R[c] in parallel with R[T], I am putting R[c] in parallel with -R[T], where -R[T] is obtained from the denominator of the transfer function when the denominator is set to zero.

R[L] is the load resistance. It is included within R[T]. It is not used for the output impedance, but it will be used for the input impedance. The OP wanted to calculate that, too. We never got around to doing that yet, although the formula is in the attachment on post #40.

RL appears to be the load, which would mean if we knew what RT was we would calculate RL from:
RL=(Rc*RT)/(Rc-RT)

Sure, but R[L] is not the unknown, it is a given. It is not used for the output impedance, but for the imput impedance.

In short, you wrote one thing and meant another thing several times now, so you cant expect anything but confusion.

No, you intrepreted what I wrote wrong, that is why you are confused.

So you are still left to explain by what mechanism you are allowed to put Rc in parallel with RT. If you want to refer to something on the web that would be fine with me.

No, not the R[T] from my definition, -R[T] calculated from the denominator of the transfer function when the denominator is set to zero. Until you understand the previous sentence, you will be confused.

Perhaps it be better to start with a different fresh problem. Something fairly simple, but not trivial. I will let you choose one.

Ratch

 

[MrAl]

QUOTE TO READ
Rx=a+b*c+1
In the above equation for output impedance, if you want to assume that 'c' is zero,
then the output impedance becomes a+1.
END QUOTE TO READ

Ratch,

If you read the above QUOTE TO READ tell me what the output impedance is.
Is it "Rx" or something else ??

MrAl,

Yes, I did define R[T]=R[c]||R[L], ignoring h[oe]. And I am saying that Rout, the output

impedance, is -R[T]||R[c], where -R[T] comes from the denominator of the transfer function when

the denominator is set to zero. I am NOT saying that the output impedance is R[T]||R[c].

Well if you want to say NOW that the output resistance Rout=RT||Rc that's fine, but
dont say that i misinterpreted your information when you presented it the way you did.
You solved for RT which was not the output resistance yet you stated clearly that is
was, so there was no other way to 'interpret' that. The attachment is a snap shot
of your own written attachment. You are clearly referring to the 'above' equation
when you talk about output impedance, and you even go as far as to calculate the
"output impedance" from the equation for -RT with hie equal to zero, and then state
that is the output impedance. See how misleading that can be?

I am not putting R[c] in parallel with R[T], I am putting R[c] in parallel with -R[T], where

-R[T] is obtained from the denominator of the transfer function when the denominator is set to

zero.

Yes, NOW you are putting Rc in parallel with -RT, but that's not what you did before as
the attachment clearly shows, and that's the reason for the misunderstanding. That's
what i am trying to get through to you.

R[L] is the load resistance. It is included within R[T]. It is not used for the output

impedance, but it will be used for the input impedance. The OP wanted to calculate that, too.

We never got around to doing that yet, although the formula is in the attachment on post #40.

Yeah, what is that "-Rg" supposed to be anyway, and why are you solving for it?
I dont get that at all, sorry.

Sure, but R[L] is not the unknown, it is a given. It is not used for the output impedance, but

for the imput impedance.

Huh??? It is a given? And where is it 'given' ?

No, you intrepreted what I wrote wrong, that is why you are confused.

Sorry have to chuckle a little here, because there was no other way to interpret it.
If you read my above QUOTE TO READ and the attachement, you can not 'intepret' it
any other way. Furthermore, if you calculate the output impedance with the 'new'
method you've described of putting Rc in parallel with -RT then you dont get the
result you quoted in the attachement when hie is assumed to be zero. So there is
no way you could have meant that RT was not the output impedance.

No, not the R[T] from my definition, -R[T] calculated from the denominator of the transfer

function when the denominator is set to zero. Until you understand the previous sentence, you

will be confused.

It is starting to look like you learned this a long time ago and then forgot how to
do it exactly, and that's ok really, nothing wrong with that. I am refreshing in
several areas myself.

Perhaps it be better to start with a different fresh problem. Something fairly simple, but not

trivial. I will let you choose one.
Ratch

Ok, i choose we do an exercise on writing what you really mean rather than writing something
else. That would make things go a lot smoother


Now getting back to the 'other' equation, the one above -RT which is -Rg.
Are you going to come back here now and say that that equation TOO isnt REALLY
for -Rg, but is REALLY for something else, or what?
Why are you solving for -Rg anyway?

 

[Ratchit]

MrAl,

QUOTE TO READ
Rx=a+b*c+1
In the above equation for output impedance, if you want to assume that 'c' is zero,
then the output impedance becomes a+1.
END QUOTE TO READ

Ratch,

If you read the above QUOTE TO READ tell me what the output impedance is.
Is it "Rx" or something else ??

Without a contextual knowledge of what the above equation represents, I don't know.

Well if you want to say NOW that the output resistance Rout=RT||Rc that's fine, but
dont say that i misinterpreted your information when you presented it the way you did.

No, I am not say that. I am saying that the output impedance is -R[T]||R[c], where -R[T] is derived from the the denominator the the transfer equation when the denominator is set to zero.

You solved for RT which was not the output resistance yet you stated clearly that is
was, so there was no other way to 'interpret' that. The attachment is a snap shot
of your own written attachment. You are clearly referring to the 'above' equation
when you talk about output impedance, and you even go as far as to calculate the
"output impedance" from the equation for -RT with hie equal to zero, and then state
that is the output impedance. See how misleading that can be?

No, I did not solve for R[T]. I solved for -R[T]where -R[T] is derived from the the denominator the the transfer equation when the denominator is set to zero. The way to intrepret it is to carefully read what I said in that post.

If you read the complete attachment from post #40, you will see that -R[T] represents the output impedance to the left the the rightmost resistors. I did calculate what the output impedance would be with h[ie] equal to zero, but that should not be a problem.

Yes, NOW you are putting Rc in parallel with -RT, but that's not what you did before as
the attachment clearly shows, and that's the reason for the misunderstanding. That's
what i am trying to get through to you.

I clearly showed in the attachment from post #40 that the output impedance -R[T] did not include R[c], because it was one of the rightmost resistors. That is why I needed to put it in parallel with -R[T] later after I calculated -R[T].

Yeah, what is that "-Rg" supposed to be anyway, and why are you solving for it?
I dont get that at all, sorry.

As I clearly stated in the attachment from post #40, -R[g] is the input impedance to the right of R[g], where -R[g] is derived from the the denominator the the transfer equation when the denominator is set to zero. To get the input impedance to the right of the source generator e[g], I need to add R[g] to the calculated -R[g].

Huh??? It is a given? And where is it 'given' ?

If you want to calculate the input impedance, you have to know the output impedance. I was going to assume 1000 ohms.

Sorry have to chuckle a little here, because there was no other way to interpret it.

I beg to differ.

If you read my above QUOTE TO READ and the attachement, you can not 'intepret' it
any other way.

Perhaps, but I can't see how it applies to this problem.

Furthermore, if you calculate the output impedance with the 'new'
method you've described of putting Rc in parallel with -RT then you dont get the
result you quoted in the attachement when hie is assumed to be zero.

Then that would be a failure in my method. Can you show that to be true?

So there is no way you could have meant that RT was not the output impedance.

I defined R[T] to be the parallel combination of three resistors. I calculated -R[T] by the method described in the attachment from post #40.

It is starting to look like you learned this a long time ago and then forgot how to
do it exactly, and that's ok really, nothing wrong with that. I am refreshing in
several areas myself.

You are correct in surmising that I learned this method many decades ago. Just as I learned Thevenin's and Norton's a long time ago. You are wrong, however, in thinking I forgot how to use it. Remember, I got the same answer as you did when you challenged me in post #55, so I did not apply it wrong. It also checks with a textbook on what the output impedance should be.

Ok, i choose we do an exercise on writing what you really mean rather than writing something else. That would make things go a lot smoother

Perhaps a exercise on reading and interpreting would be more in order.

Now getting back to the 'other' equation, the one above -RT which is -Rg.
Are you going to come back here now and say that that equation TOO isnt REALLY
for -Rg, but is REALLY for something else, or what?
Why are you solving for -Rg anyway?

As I said before, -R[g] is the input impedance to the right of R[g] in the circuit posted in the attachment of post #40. In that attachment, I never said that -R[t] is -R[g]. In fact, they are two different equations, one for input impedance, and one for output impedance. It is all explained in the narrative of that attachment.

I really think we should start fresh and do another problem.

Ratch

 

[MrAl]

Hello again,


If i say to you that:
"Rx is the output impedance"

Now i ask you again, what is the output impedance? If you dont know that it is Rx then you really need help


It seems to me that all you are doing now is trying to dodge the bullet, which if that's what you want to do that's certainly up to you. But all you had to do in the first place was to solve for RL and you would have ended up with a nice neat little equation that distinctly showed how to calculate the output impedance. But you insisted:

"Sure, but R[L] is not the unknown, it is a given. It is not used for the output impedance, but for the imput impedance."

but RL could be called the output impedance and then solved for explicitly and that's all that would be required. No parallel resistors later.

[assuming hie to be zero and calculating "-RT" and calling that equation the 'output impedance']
"Then that would be a failure in my method. Can you show that to be true?"
I dont think it was a failure in 'your' method, i just think you were originally taking RT (or -RT) to be the output impedance, then used that equation to to calculate the output impedance with hie equal to zero, or else you just used that equation.
To show that there is an error, all you have to do is take your 'new' equation (with the parallel Rc) and compute the 'output impedance', and it does not come out to Rf/(1+hfe) as you stated. That was another source of confusion because you were then explicitly stating that Rf/(1+hfe) was the 'output impedance' with hie equal to zero yet the only way you could get that result was if you used the equation for -RT for the output impedance. If you used your 'new' equation (which we now know is the right way) you would have found a little more complex result, not Rf/(1+hfe). If you have a problem with that, simply calculate the 'output impedance' using your new equation, which we now believe to be correct at least in the linear sense.

I just want to mention that when someone asks something like, "What is the value of Rx", the best way to show it, if you take the time to do it at all, is more or less like:
Rx=f(x,y,such_and_ such)

That why they can use their own method and come back and immediately calculate your result and compare to see if they made a mistake. If you instead come back with:
Ry=f(x,y,whatever)

and state that is Rx, or even if you dont state that is Rx but is really Ry, that just makes it more difficult for them to calculate the real required value of Rx.

In other words, if they ask for input and output impedance why not just show expressions for that:
Rin=f1(R1,2,3, etc.)
Rout=f2(R1,2,3, etc.)

That would make it a lot clearer and easier and a lot faster too

BTW, the way i came up with the output impedance was using the standard output perturbation method. One of the simplest ways is to just use a current source on the output and calculate the voltage deviation and the current deviation and then take:
Rout=dV/dI
which of course is very straight forward.

If you want to do a simpler example using GIT that you mentioned, that would be nice i guess. We can do a simple voltage divider with R1 on top and R2 on bottom fed by a voltage source Vs:

Vs o---R1---+---R2---o GND

where we take the output from the junction of R1 and R2. We want to calculate the input resistance and the output resistance (call it impedance if you like). This should be simple but lets see how it goes

Before we depart from the transistor circuit however i think we should clear up the equations a little. Make them into explicit equations for Rin and Rout.
Also, a non linear analysis using some Spice data would be very nice too, to back up the linear method.