Hello again Wizard,
That's very good. With this new post you have just made this concept a LOT more interesting, but you still have a little more work to do.
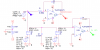
Note that when we have an amplifier with a gain say G, the output is proportional to the gain G as:
Vout=G*Vin
This is a very simple concept, i am just spelling everything out to be clear.
This means that if G=5 and Vin=1 we get:
Vout=G*Vin=5*1=5
but if Vin=2 we get:
Vout=G*Vin=5*2=10
So the main point here is that G holds for both inputs, 1v and 2v, and if we have two gains G1 and G2 that we believe are the same, then we would have:
Vout1=G1*Vin
and
Vout2=G2*Vin
and with G1=G2 we would always have:
Vout1=Vout2
no matter what we choose for Vin (within reason).
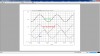
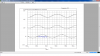
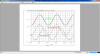
To to prove that G1=G2 we must show more than one result for two different Vin's, and this means we need to show two different simulations but without changing anything except the value for Vin. (Note more than two would be even better as two alone could still coincide with a parabolic behavior while with three that would be very difficult to stumble on by accident).
So you have to change Vin to some other value that is significantly different than it was for the first run, and then do a second run, at the very least. If you wanted to you could do a stepping of Vin over several different values and if the output of the two circuits agree, then i think you would have proved that the two are equivalent. However, doing one single simulation with only one value for Vin does not prove anything except that you can set the gain to be the same for one value of Vin

So do a couple more simulations with different Vin and hopefully you can prove this once and for all. I am interested to see the results also.
One more small note...
You also have to be careful that some feature of one of the models and/or the values for the components dont dominate the response. If this occurs then the feature we are looking for will never show itself. For example, if you are designing a low pass filter with cutoff 1.2kHz and you follow it with a low pass filter with cutoff 1kHz, it might look like the 1.2kHz filter is working when really it could just be a single straight piece of wire with the 1kHz filter doing all the work. If you look closer you will find the response doesnt follow the right pattern, but it may take very accurate values to see it. If the values are chosen so that they do not force behavior that coincides with other behaviors, then it will be easy to see.
For this reason the Vin test values should be significantly different but the capacitors should be chosen so that the expression with the capacitors comes out significantly different than a reduced complexity expression such as C2/C2 for example, or worse yet, C1/C2 (although i doubt this can happen too easily).