Hello guys,
>So, I guess you have to do something a little fancy:
http://www.wolframalpha.com/input/?i=rms
Yes, it seems like the same thing as this (just in lamens terms):
http://www.analytictech.com/mb313/rootmean.htm
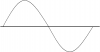
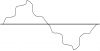
HOWEVER, something still doesn't make sence. First of all, please take a quick look at the graph in my attachment below:
If we go by the method explained in my latter link above, then let's assume that Voltage at 100% will be 100V peak. Now, let's do this:
Step#1 (square all values of the top part of the AC wave):
V @ 10% = 10 Volts ² = 100
V @ 20% = 20 Volts ² = 400
V @ 30% = 30 Volts ² = 900
V @ 40% = 40 Volts ² = 1600
V @ 50% = 50 Volts ² = 2500
V @ 60% = 60 Volts ² = 3600
V @ 70% = 70 Volts ² = 4900
V @ 80% = 80 Volts ² = 6400
V @ 90% = 90 Volts ² = 8100
V @ 100% = 100 Volts ² = 10000
V @ 90% = 90 Volts ² = 8100
V @ 80% = 80 Volts ² = 6400V
V @ 70% = 70 Volts ² = 4900V
V @ 60% = 60 Volts ² = 3600V
V @ 50% = 50 Volts ² = 2500V
V @ 40% = 40 Volts ² = 1600V
V @ 30% = 30 Volts ² = 900V
V @ 20% = 20 Volts ² = 400V
V @ 10% = 10 Volts ² = 100V
Step#2 (Sum all values):
Sum of all values is: 67000
Step #3(Do the average of all these values):
Average: 67000/19 slices = 3526
Step#4 (Do the square root of the average):
RMS = √3526 = 59.38 Volts ?????
59.38 volts is *NOT* the rms value of 100V peak????
RMS is supposed to be 70.7 Volts ?????
Can someone explaine this discrepentie. Confused!
r