zachtheterrible
Active Member
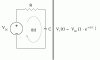
It is very simple to find how long it will take for the capacitor to charge to one time constant or 63% of the supply: t=RC.
But say that I want to figure out how long it will take for my capacitor to charge up to 20% of my 3 volt supply (.6v) given R and C.
Please help, thanx :lol:
But say that I want to figure out how long it will take for my capacitor to charge up to 20% of my 3 volt supply (.6v) given R and C.
Please help, thanx :lol: