Difference between mixing and adding a frequencies [audio]

[zhexy]

I'm a composer, curious about everything under the hood. In terms of math and physics - I'm newbie.

Recently, I stepped into the field of frequencies. There is a term "Mixer", that is dedicated to "mix" frequencies/audio signals together.
Following this thread I have a question:
Why do we need a mixer, if in term of math we can simply add frequencies?

I bring the following materials to the table.
I know that any sound has a harmonics. Harmonics I understand as a frequency on top (or below) given base frequency (I'll disregard amplitude and phase shift). So, in my head, we can get resulting frequency by adding two, like:
\( f_{a}+f_{b}=f_{c} \)

But mixers, as said, is a way to "multiply" frequencies/audio signals.

So, if I pluck an imaginary ideal string (disregarding the length) in an ideal imaginary space with no reflections, I should read an input as in the formula above, shouldn't I?

This is the screenshot I made, showing mixing formula found in the mentioned thread, and addition formula.

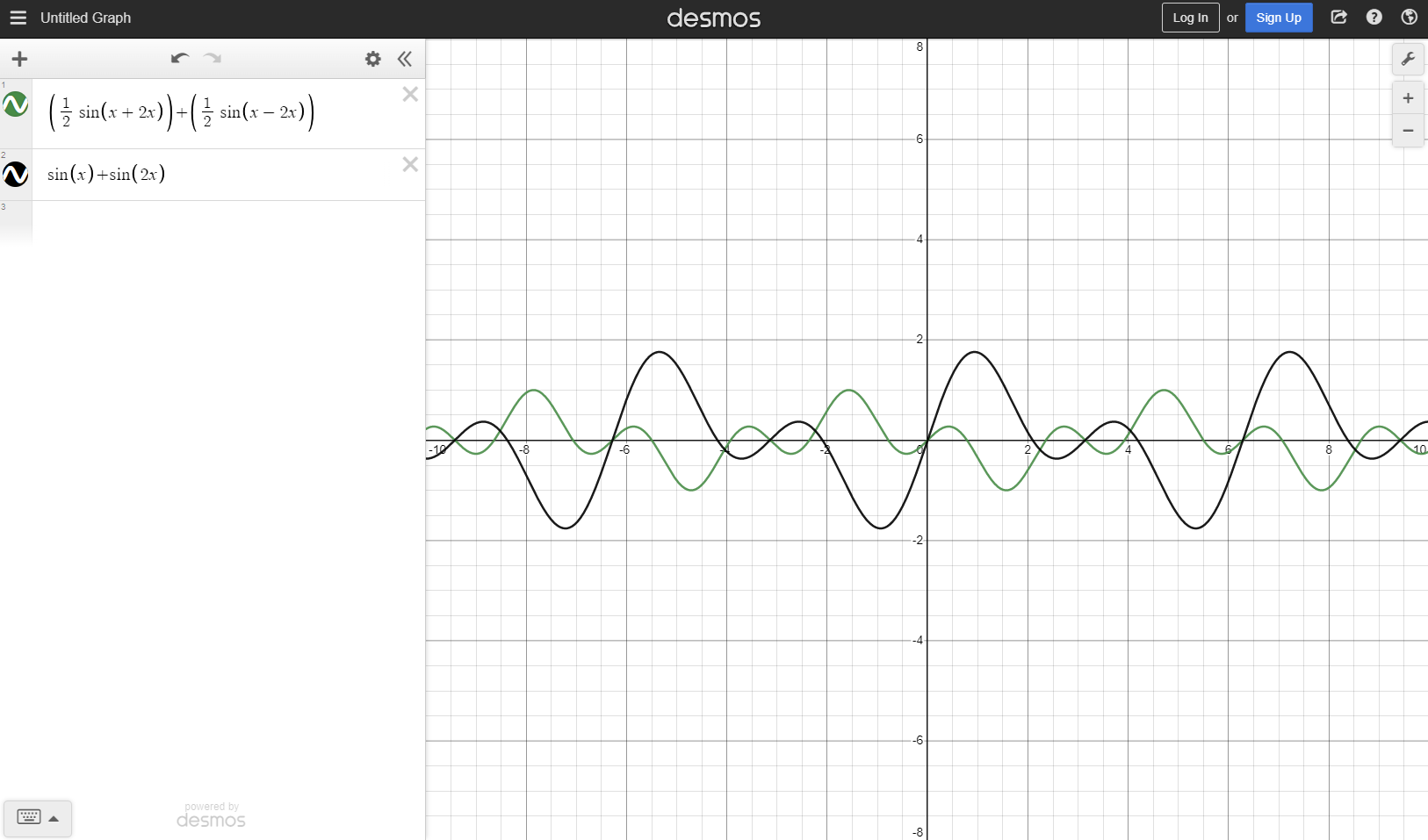
I would be a very thankful for the replay, explaining to me, what is the difference, or an error in my thoughts.

Thank you!

 

[danadak]

Adding frequencies -

http://spiff.rit.edu/classes/phys207/lectures/beats/add_beats.html

Square Wave from Sine Waves - MATLAB & Simulink Example

This example shows how the Fourier series expansion for a square wave is made up of a sum of odd harmonics.

www.mathworks.com

02. Mixing Waveform - UltraMixer

Here you can learn more about pitching with the waveform and other setting options for the sound wave.

ultramixer.com

Regards, Dana.

 

[JimB]

There is a term "Mixer", that is dedicated to "mix" frequencies/audio signals together.

The word "mixer" has two different meanings.

In the audio world, a mixer simply adds (mathematically) two or more signals.
If we examine the signals on the output of the mixer, we will see only those signals which are fed into the mixer input.

In the radio world, a mixer multiplies (mathematically) two signals.
In this case if we examine the output signals from the mixer we may see that the original signals which were fed into the mixer are not there on the output.
But, new frequencies have been created in the mixer.

That is what I was trying to demonstrate in the old thread:

Following this thread

JimB

 

[rjenkinsgb]

A Jim says.
But note that it relates to signal voltages not directly to frequencies, though the end result may have different frequency components after voltage multiplication.


"Mixing" as in an audio mixer is just summing voltages.

The instantaneous signal voltages are added together, with some gain or attenuation applied. You hear all the original input signal sounds together, as you would when hearing several different sound sources directly, at the same time.


Mixing in the technical sense, as used in radios etc., means the instantaneous voltages are multiplied together, with gain adjustments or loss.

The audio equivalent of that is a "Ring modulator" such as used in music synthesisers.

The output result of that consists of both the sum and difference of the two input signal frequencies.
Think "Dalek voice" as one example, with speech plus a fairly low audio frequency.

Direct frequency adding or shifting without both sum and difference is a lot more complex.

 

[Musicmanager]

I think you need to be cautious of using the term 'harmonics' in relation to sounds created electronically because those sounds are purely the result of a mathematical input calculated to produce a frequency through an electronic process.

In the musical world, using instruments that generate sound through vibration, harmonics are produced by interrupting the natural wavelength with a node that allows the vibration to continue either side of that node.

For example, a Violin string left open and vibrated with a bow will produce a single sound based on the wavelength generated by the length of the string (fundamental or 1st generation harmonic). If a finger presses that string onto the finger board/neck of the instrument, the string length and therefore, the wavelength generated will change (still fundamental or 1st generation harmonic). However, if the finger touches the string but does not press to the finger board, the string length remains but the resultant sound will be a 2nd generation harmonic. It is possible although very difficult to have the fundamental and 2nd generation sound at the same time.

That is an over-simplification of the principle, and this may give a better understanding .. .. .

The Physics Classroom Website

The Physics Classroom serves students, teachers and classrooms by providing classroom-ready resources that utilize an easy-to-understand language that makes learning interactive and multi-dimensional. Written by teachers for teachers and students, The Physics Classroom provides a wealth of...

www.physicsclassroom.com

Physics Tutorial: Fundamental Frequency and Harmonics

Each natural frequency that an object or instrument produces has its own characteristic vibrational mode or standing wave pattern. These patterns are only created within the object or instrument at specific frequencies of vibration. These frequencies are known as harmonic frequencies, or merely...

www.physicsclassroom.com

Once the principle is understood, it is possible to create harmonics electronically, but they would be artificial because you would need to imitate the fundamental and the 2nd generation sound as separate inputs.


MM