In general what we care about in control systems is their behaviour
to varying electrical conditions, that we maintain design goals for
these changes in control loops (sensors) and environmentals that affect
the control loop. That control loops do not saturate in their handling
of signals for example.
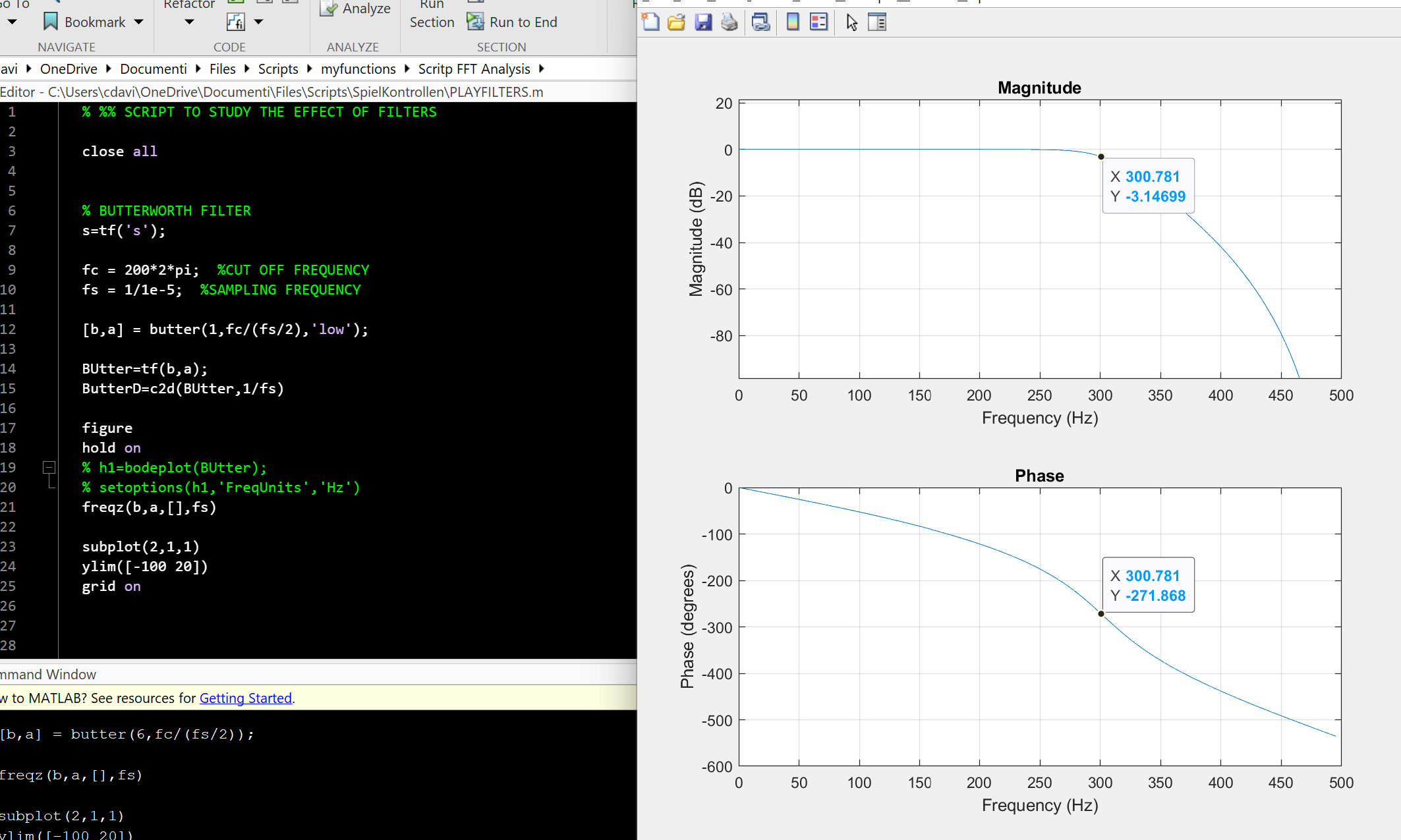
Classic loss of control can be chaotic, oscillation, or breaking desired transfer
functions behaviour. Like classic motor boating in audio gear. One key theory is :

en.wikipedia.org
Note discussion is not confined to linear systems, there is a rich area of study,
tons of papers over the years in IEEE, of studies and benefits of non linear
goals and work. I used a non linear filter in a PLL feedback loop to decrease
settling and acquisition in a low freq loop where delays accentuated by pole
frequency locations of the system aggravated the loop response.
Regards, Dana thank you very much Donna for your response