Thevenin Resistance

[JeanTech]

Hi There

How would one go about determining the Thevenin resistance in the following circuit? Would it be correct if I turn off the 2 A source (thus it becomes an open circuit with no current flowing through) and then use nodal analysis to determine the in going current and then use it to calulate R(Thevenin) using Ohm's Law?

What would the answer be?

Thanks in advance
JeanTech

 

[MikeMl]

Same way you always do it: Calculate the open circuit voltage from a to b. Short a to b, and calculate the current.

I'm puzzled by your diagram.

Is the current source = square root of 2 = 1.414sin(wt) ?
Is the voltage source = 2sin(wt)?

 

[JeanTech]

Same way you always do it: Calculate the open circuit voltage from a to b. Short a to b, and calculate the current.

I'm puzzled by your diagram.

Is the current source = square root of 2 = 1.414sin(wt) ?
Is the voltage source = 2sin(wt)?

Hi Mike

Yes, the current source is square root of 2. However I think the voltage and current source is a cosine function as it is a real number or am I incorrect in my assumption?

 

[MikeMl]

Hi Mike

Yes, the current source is square root of 2. However I think the voltage and current source is a cosine function as it is a real number or am I incorrect in my assumption?

Since no phase shift between the current source and the voltage source is indicated, I would assume that they are both either sin(wt) or cos(wt); not one of each.

 

[Ratchit]

JeanTech,

"How would one go about determining the Thevenin resistance in the following circuit?"

You mean impedance, because there are reactances involved.

"Would it be correct if I turn off the 2 A source (thus it becomes an open circuit with no current flowing through) and then use nodal analysis to determine the in going current and then use it to calulate R(Thevenin) using Ohm's Law?"

If all the sources were independent, then you could say the Thevenin impedance would be 8 ohms of resistance in parallel with 8 ohms of capacitive reactance. But the Thevenin and Norton methods by themselves are invalid for circuits with dependent sources. The combination of Thevenin-Norton does give the correct equivalent impedance. See the derivation of Voc and Isc in the attachment. Notice that the Thevenin impedance is negative, which means that if you apply a positive voltage to the circuit, the circuit will try to push a current into your voltage source. This is due to the counter voltage produced by the dependent voltage source.

Ratch

 

[steveB]

... But the Thevenin and Norton methods by themselves are invalid for circuits with dependent sources.

That is what is usually taught.

I thought I would provide an unpublished (actually rejected) paper about applying Thevenin to cases with dependent sources. At the AAC forum t_n_k provided a copy of this paper, and I think The Electrician is the one who originally made it available to us. It is an interesting paper, and worth being aware of.

My view is that the reviewer who recommended rejection of this paper did not get the analysis correct. At the other forum, I made the following comment when I read this.

Wow, did you see that trick the reviewer played? He claimed that a resistor can be considered as a dependent voltage source, OR as a dependent current source. Then he sets up a circuit that forces constraints that allows only one voltage AND one current in the resistor R1. Hmmm, don't voltage sources allow arbitrary currents, and don't current sources allow arbitrary voltages?

Note that V1=(I1+I2)/g and the current through R1 is (I1+I2)/(R1 g). Both values depend on parameters that are pre-specified. So, the resistor R1 acts simultaneously as a voltage source and as a current source, which doesn't give any freedom in the external loading.

Consider a case where I1=I2 , not equal to zero, and R3=R2. This circuit is symmetrical, so V1 must be zero, hence the current in R1 is zero. This also means that the dependent current source has no current, and the currents in R2 and R3 are equal to zero. So, we have two current sources I1 and I2 pumping current into the circuit, but that current doesn't flow into any of the allowed current paths.

Section II of the paper gives the proof. To convince yourself, you need to understand the proof, and for any given circuit you need to make sure that your conditions are meeting the starting assumptions of the proof. This procedure might or might not be straightforward for a particular circuit. Or, you can prove your particular case by noting that you get the correct answer using the method. Note the final quote as follows.

"The above proof does not imply the controlling variables of a dependent source are deactivated when applying superposition to the source. Only the output of the source is set to zero. This procedure makes it is possible to write circuit equations by considering only one source at a time or to one side of a source at a time. This considerably simplifies the use of superposition with dependent sources compared to the way that it is presented in most circuits texts."

 

[The Electrician]

Steve, I don't see a link to the paper; here it is:

https://users.ece.gatech.edu/mleach/papers/superpos.pdf

While retrieving the link with a Google search, I noticed another paper of which I was unaware. I'm just in the process of reading it now:

https://eprints.soton.ac.uk/271202/1/superposition.pdf

 

[steveB]

Thanks,
I thought I attached the paper, but I guess I forgot.

I'll read that new paper too, thanks for that also.

 

[Ratchit]

To the Ineffable All,

You might find it of interest to read what I said about the reviewer, and the late, great Prof. Leach over a year ago.

https://www.physicsforums.com/showthread.php?t=549933

Ratch

 

[steveB]

I'm happy to see this newer paper. It ties up some loose ends and gives the well deserved credit to W. Marshall Leach, Jr. and gets it into the official scientific literature.

 

[Ratchit]

I'm happy to see this newer paper. It ties up some loose ends and gives the well deserved credit to W. Marshall Leach, Jr. and gets it into the official scientific literature.

As interesting and informative as those two documents are, I have to wonder why they are referenced in this thread. This thread started out answering a question about the validity and application of Thevenin's theorem, whereas Prof Leach's paper and its followup addresses the validity of superposition. Thevevin's theorem is only mentioned incidently in the solution of one problem, and not mentioned at all in the second paper. Therefore, I believe we wandered off the reservation a bit.

Ratch

 

[steveB]

As interesting and informative as those two documents are, I have to wonder why they are referenced in this thread. This thread started out answering a question about the validity and application of Thevenin's theorem, whereas Prof Leach's paper and its followup addresses the validity of superposition. Thevevin's theorem is only mentioned incidently in the solution of one problem, and not mentioned at all in the second paper. Therefore, I believe we wandered off the reservation a bit.

It does wander off a bit, and apologies to the OP if this drifting is unwelcome. My hope is that being aware of this information might be useful at some point later in his studies.

To answer your implied question of why they are referenced, the second document was most likely found by The Electrician while he was searching for the first one that I forgot to provide the link for, and if the first one is mentioned, then the second one becomes very relevant, given the first paper is a rejected paper and the second is an accepted paper.

The reason why I decided to refer to the first paper was basically because your wording triggered my memory about this paper; and, as you say, it is interesting and informative. Not that everything interesting and informative belongs in this thread, but it did seem relevant somewhat because Thevenin's theorem is derived using superposition as its prime ingredient, so the two concepts are linked.

 

[MrAl]

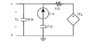
Hi There

How would one go about determining the Thevenin resistance in the following circuit? Would it be correct if I turn off the 2 A source (thus it becomes an open circuit with no current flowing through) and then use nodal analysis to determine the in going current and then use it to calulate R(Thevenin) using Ohm's Law?

What would the answer be?

Thanks in advance
JeanTech

Hi,

Well, the first thing we note right away about this circuit is that we have a lot of stuff in parallel. The only things not in parallel are the 8 ohm and the 2Vx dependent source. However, if we replace the 8 ohm and 2Vx source with it's Norton equivalent, we end up with everything in parallel. Then we can use a well accepted theory of applying a non zero excitation voltage or currrent, calculating the opposite quantity, then dividing voltage by current to get the resistance or impedance.

To see how easy this is for this circuit, lets look at the currents through each element after we make the transformation of the 8 ohm and 2Vx source to a parallel Vx/4 current source and a parallel 8 ohm resistor when excited by a 1v voltage source. Note also that the second capacitor does not matter because it is in series with a current source.

From left to right, we have first the -j8 ohm load and the current is:
-1/8j amps, which comes out to j/8 amps, so i1=j/8.

Next we have the sqrt(2) amp source, which is of opposite polarity so we have:
i2=-sqrt(2)

Next we have the 1/4 amp Norton current source, which is also opposite polarity so we have:
i3=-1/4

Next and finally we have the parallel 8 ohm Norton resistance, so we have:
i4=1/8

Now we add them all up:
iTotal=i1+i2+i3+i4=-sqrt(2)-1/8+j/8

Since we used a source of 1v for the calculation, we divide to get the impedance:
Z=1/iTotal=1/D, where D=-sqrt(2)-1/8+j/8

Now since there is an imaginary term in the denominator, we calculate the conjugate of D:
cD=-sqrt(2)-1/8-j/8

and calculate the denominator of the impedance Z by multiplying cD times D:
ZD=cD*D=65/32+1/2^(3/2)

and the numerator of the impedance Z by multiplying the voltage times cD, and since the voltage was 1v we get:
ZN=cD

as the numerator.

So the impedance is:
ZN/ZD=(-sqrt(2)-1/8-j/8)/(65/32+1/2^(3/2))

and simplifying this and converting to an approximate floating point representation we end up with:
Z=-0.645426-0.0524152*j

as the complex impedance with each part rounded to 6 significant digits.

 

[Ratchit]

MrAl,

Two questions for you.

1) Why don't you get the same answer as I do?

2) How would you calculate the impedance of the circuit if 2Vx were an independent source?

Ratch

 

[MrAl]

Hello Ratch,

Well, i may be making a mistake here. It looks like we have to calculate an equivalent Thevenin voltage source and equivalent Thevenin series impedance. Thus the impedance might change with input.
But what really bothers me is that the circuit has positive feedback, and with a,b open circuit and the sqrt(2) current source being the only excitation, it looks like what may happen is the current source causes current to flow through j8 ohm and 8 ohm, until Vx across j8 ohm rises slightly, at which time 2Vx rises two times as high causing more current to flow into the node at 'a'. That in turn causes Vx to rise even more, which in turn causes 2Vx to rise more, and so on and so forth until node 'a' reaches either a vary high value or infinity.

So my question to you is, how did you calculate the open circuit voltage, and was that at node 'a' ?
I went over your inset in your other post but it was not that clear because for example you have a current on the left side of an equation or transformation and a voltage on the right side, which doesnt make sense in itself, but im sure you have an explanation.
So please state how you calculated the open circuit voltage for this circuit, and try to explain it as clearly as possible. We can then move on from there.

This circuit reminds me of the op amp circuit i think we all looked at a while ago, not that long ago. Or maybe it was a transistor circuit. But it had feedback and we wanted to calculate the input impedance and what happened was we found that it varied with input level. So this would require a Th source and Th impedance.

Im half asleep right now though so i'll have to take a better look at this later today or tonight sometime.

 

[Ratchit]

MrAl,

Just so we are on the same page, we want to find the impedance across terminals a-b. If the circuit contained only independent sources, we could just zero out the voltage sources, open the current sources, and calculate the Thevenin impedance directly. But because of the dependent voltage source 2Vx, neither Thevenin's or Norton's theorems works by itself. So instead of trying to discern the impedance by looking inside the circuit (direct calculation after substituting the source impedances), we have to look away from the circuit and see what the circuit presents to the outside world (Voc, and Isc). We do this by the combination of Thevenin and Norton, which is the Thevenin-Norton theorem. The Thevenin-Norton states that if the outside world sees the open circuit voltage (Voc), and the shorted current (Isc), then the impedance of a linear circuit has to be a unique value of Voc/Isc. That means the Thevenin-Norton works regardless of dependent sources being present or not.

I first calculated Vx with the terminals a-b open, which is the same as Voc, by straight forward node analysis, as shown by the inset of post #5. Then Isc is simply the shorted current coming from the independent source. Finally, division give the circuit impedance.

I already mentioned that the impedance of this circuit has a negative real component. That means that any voltage source applied to Vx will receive a backwards current supplied by the independent current source and the dependent voltage 2Vx. That is the positive feedback you mentioned. I calculated the voltage and current across and through a-b, so I don't know what you mean by a current on the left side and a voltage on the right side. Anyway, the Thevenin-Norton theorem is the way to go with this problem.

Ratch

 

[steveB]

Ratch,

I believe your answer is correct.

There is something particular interesting about this circuit. The 8 Ohm resistor in series with the 2Vx dependent voltage source seems to behave as a -8 Ohm resistor in this circuit. That allows a simplified view of the circuit and removes the dependent source from the analysis. So looking back into the circuit we see the -j8 Ohm capacitor in parallel with a -8 Ohm resistor, which gives the correct Rth, and the Vth voltage is simply the sqrt(2) current source driving that impedance, which also agrees with the answer given.

Another simplification is to just short out the -j7 Ohm capacitor because it is in series with the infinite impedance of an ideal current source. This fact is obvious in your analysis Ratch, but the OP should keep an eye out for these simplifications because they make the problem look simpler and can take stress away when doing and exam.

 

[Ratchit]

steveB,

One has to be careful with dependent sources, they are tricky. The reasoning that justifies the answer might be faulty even though the answer just coincidently is correct. I, personally, would grind through the calculations I know are correct than trust myself not to overlook some flaw in my shortcuts. But to each, h(is/er) own method.

Ratch

 

[steveB]

I don't disagree. I just thought it was an interesting fact that the arrangement creates a Vx of opposite polarity on the 8 ohm resistor, and the entire branch is across the Vx voltage, so it effectively turns the 8 Ohm resistor into a -8 Ohm resistor across the branch.

 

[MrAl]

Hello again,

After reviewing this problem again and seeing that you two agree with each other, then if you agree that the Thevenin voltage source is equal to:
Vth=sqrt(2)*(-4-4*j)

and the Thevenin series impedance is equal to:
Zth=-4-4*j

then i now agree with both of you.

I also agree that Steve's observation about the 8 ohm resistor being converted into a negative 8 ohm resistor is an accurate and reasonable one. The simplification comes about simply because this circuit has voltage sources involving Vx on both sides of that resistor, as the left side of 8 ohm is always related to the right side of the 8 ohm through Vx. Using a negative 8 ohm means we dont need the Norton current source anymore. With the Norton current source (replacing 2Vx), then the 8 ohm has to stay positive.

I almost forgot to mention that it looks like this circuit might belong in the "Theoretical Only" section of our libraries. That's because it looks like with even the smallest DC offset voltage present at the input the circuit could ramp to an infinite response, which would mean it would latch up to the highest or lowest possible operating voltage and stick there. You could look at this too if you wish.