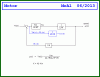
Hi MrAl
I basically agree. It's important to have units that match. I think you meant to divide to find the time constants? For example, τ=L/R, not τ=L*R. In making the ratio r, a unitless definition is better than r=J/L because J/L has units, and you can't compare something with units to 1 meaningfully in general.
However, I disagree that "Comparing La to Ra does not help", because this seems to be the exact argument that the textbook is making, but obviously it is sL compared to R. Hence, this is the best answer to give to PG, unless you disagree with the treatment given by the book. Also, comparing Jo and bo suffers from the same problem of units that don't match. We must compare sJ with b, to compare, and this depends on frequency. However, the book treatment assumes bo and Jo are both important and they are retained in the analysis.
Hello again Steve,
Yes i meant to state this:
[LATEX]r=\frac{J\,Ra}{La\,b0}[/LATEX]
which is easier to understand as:
[LATEX]r=\frac{J/b0}{La/Ra}[/LATEX]
From the above you can see i am comparing the two times constants which is more exact than simply comparing the inertia to the inductance.
We sometimes shorten this in discussion to r=J/La even though they do not have the same units, but of course that is not as correct.
But i can not find a way to state what we are talking about in terms of only La and Ra because La and Ra are ONLY responsible for the current rise time, and if the current rise time is short compared to the time it takes to overcome the rotational inertia then we still dont have to consider La in the approximation to the response.
You are right in that it does not matter to me whether or not the 'book' wants to admit to this or not, because it can be easily proved by plugging some numbers in and calculating the response time with a few different values for each component.
For a really quick example, if L=1 and R=1 and J=100 and f=1, we have the motor current rise to very near max in 5 seconds, which means the input power is already at a max and the torque is at a max and is now constant, while it takes the rotational inertia about 500 seconds to be nearly completely overcome, so we have as a very rough estimate 500+5=505 seconds to spin up to full speed, and making L=10 and R=10 we see the same thing except the max current is now less, so takes even longer for the rotational inertia to be overcome.
But also, if we keep the same L and R and make J=1 and f=1 as before we see that the current comes up in the same time as before, but now it takes much less time for the inertia to be overcome, so the motor spins up faster.
So with L=1, R=1, J=10 and f=10, we see a long time to spin up, but with L=1, R=1, J=1, and f=1, we see a short time to spin up yet we see the same comparison of L and R.
Also, what did you mean when you wanted to use wL to compare to R, what do you intend to make 'w' here?
Better numerical example follows...
The true test is:
[LATEX]\frac{\partial f(t)}{\partial \,var}[/LATEX]
where 'var' is the variable in question and f(t) is the speed with time, and we should find something like this:
[LATEX]\frac{\partial f(t)}{\partial \,var1}>\frac{\partial f(t)}{\partial \,var2}[/LATEX]
Start with L=0.001, R=1, J=1, f=1, speed after 1 second is: 0.432332 rads/second.
Now change L=0.002, speed after 1 second is: 0.432332 rads/second.
Now put L back to 0.001 and change J=2, speed after 1 second is 0.315968 rads/second.
Now leave J=2 and make L=0.002 again, speed after 1 second is 0.315876 rads/second.
So doubling the inductance did not change the speed after 1 second much (it did change out to many decimal places) but
doubling the rotational inertia made a much bigger difference in the speed after 1 second.
It also is worth noting that the response exponential multiplier time exponent turns out to be the average of the reciprocals of the two time constants, where one is L/R and the other is J/f:
e^-at, with a=0.5*(R/L+f/J)
So although R/L (or L/R) does in fact affect the spin up time, it does not act alone.