Pseudo-Random number generator with a complete numerical sequence

[Fra93]

I would like to present a personal invention of mine.

It is a circuit that can produce a pseudo-random sequence with a period of 2^n numbers, where n is the numbers of registers.

The classical approach to generate pseudo-random numbers is to use Fibonacci or Galois linear-feedback shift register (LFSR) but the period of the generated random sequence is limited to 2^n - 1 numbers.

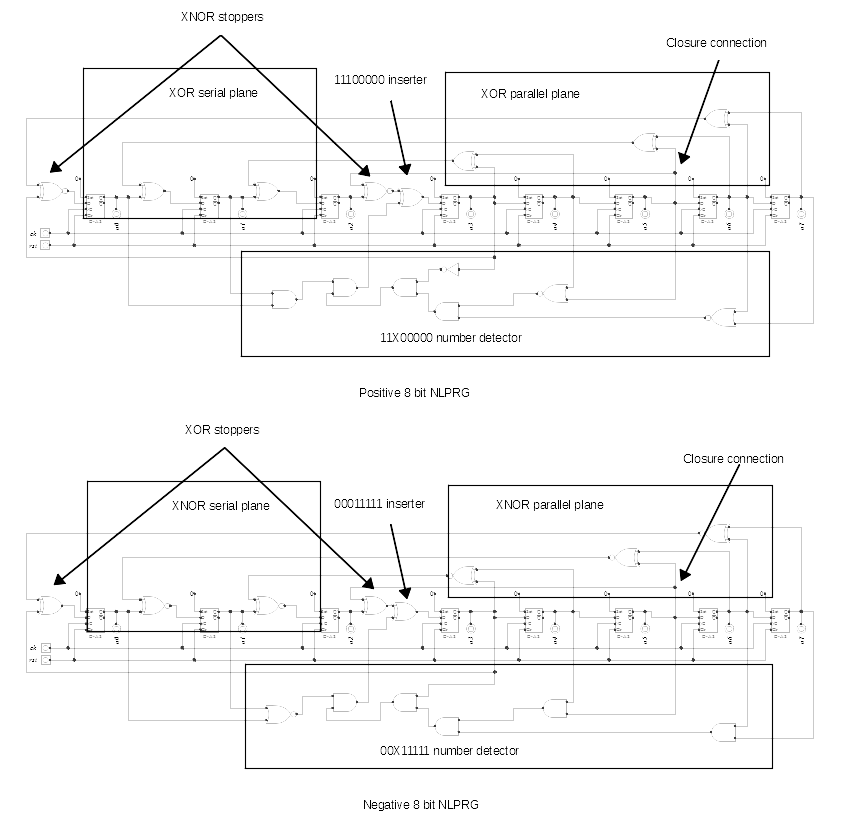
Furthermore, with the methodology I am proposing there are more circuit types that produce a complete sequence, therefore, it is more resistant to mathematical attacks.

Here it is a link to the blog post:
**broken link removed**

Here to links to the code if someone wants to try it out:
https://gitlab.com/francescodellanna/nlprg
https://opencores.org/websvn/listing/nlprg/nlprg

I will post in the future the circuit with multiple bit lengths ( from 3 to 16 bits ).
Any feedback is really appreciated.

 

[BobW]

So, you have to double the amount of logic so that your 16 bit SRNG can generate just one more state?
65536 instead of 65535? The economics seem doubtful.

 

[Fra93]

There are few things to consider besides power consumption:

1. It produces a complete sequence.
2. There are more possible permutations of complete sequence typologies, which makes harder to predict the sequence.
3. It can be optimized by making the transfer function more complex and therefore more secure.

It is extremely easy to break the pseudo-random sequence produced by LFSRs. This slightly more secure approach might be worth the power budget.

A Bijective transfer function for pseudo-random number generation will probably find its application in cryptography.

I researched on the topic and I did not find any equivalent circuit "a shift register circuit" with a complete sequence.
If you find a simpler way to do that please let me know.

Considering the aspect of power.

With normal LFSRs you generally need to perform a check on the seed to avoid the insertion of the dead code in the registers.
If the injected seed is wrong, than you need either to correct the fault or live with it. This is generally extra circuit that needs to be implemented in practical applications.

I hope this answer your question.

 

[BobW]

Thanks for the reply. Most of the LFSRs that I'm aware of, have only the value 0 as the dead value, and that is easy to detect. I do understand having a missing value could cause difficulties in certain applications.

 

[nsaspook]

More secure, unlikely.

Fibonacci CSRNG's are perfectly fine circuits and have been used since the 1950's in tube type digital devices for cryptography that's never been broken unless you have the actual keycard.

http://www.jproc.ca/crypto/kwr37.html

These tube based devices were used until the late 1980's.
http://gocs.info/pages/technik/deu/3-kw-46-0.htm

 

[Fra93]

There are many algorithms to predict "break" the sequence.

Here is the most used algorithm to do so https://en.wikipedia.org/wiki/Berlekamp–Massey_algorithm .

Every pseudo-random number generator can be broken, the right question is how many numbers in a sequence you need to do so.

As a role of thumb if you have more topologies that can produce a complete sequence, it gets harder to predict the circuit topology, therefore, the sequence is more secure.

I know that LFSR are perfectly fine, but I do not understand why it is unlikely that the circuit I am proposing is less secure.
Do you have some evidence? That it is not ( the other ones have always been used since the 1950 ).

If you want to test or break the algorithm you are welcome and encourage to do so.

Here I can give you a list of nlprg, and the code is given at this link: https://gitlab.com/francescodellanna/nlprg/-/tree/master/examples

 

[BobW]

Have you subjected it to the Diehard or Die-Harder test suite?

Robert G. Brown's General Tools Page

 

[Fra93]

No, thanks for the suggestion. I will look into it and post here the results.

 

[nsaspook]

There are many algorithms to predict "break" the sequence.

Here is the most used algorithm to do so https://en.wikipedia.org/wiki/Berlekamp–Massey_algorithm .

Every pseudo-random number generator can be broken, the right question is how many numbers in a sequence you need to do so.

As a role of thumb if you have more topologies that can produce a complete sequence, it gets harder to predict the circuit topology, therefore, the sequence is more secure.

I know that LFSR are perfectly fine, but I do not understand why it is unlikely that the circuit I am proposing is less secure.
Do you have some evidence? That it is not ( the other ones have always been used since the 1950 ).

If you want to test or break the algorithm you are welcome and encourage to do so.

Here I can give you a list of nlprg, and the code is given at this link: https://gitlab.com/francescodellanna/nlprg/-/tree/master/examples

Cryptographic random number generation is
a harder problem. One of the necessary properties is the inability to sequence future output from past sequences.

https://www.johndcook.com/blog/rng-testing/

For cryptographic applications, statistical quality is necessary but not sufficient. A random number generator can have excellent statistical properties and yet be cryptographically weak.

For example, while the popular Mersenne Twister is suitable for statistical applications, it is not appropriate for use in cryptography because its future output can be predicted from past output by solving a system of linear recurrence equations.

The NIST Statistical Test Suite (STS) is recommended for testing CSPRNGs (cryptographically secure pseudorandom number generators) though it in no way guarantees an RNG is secure. The Mersenne Twister, for example, passes STS without any issues. STS is not a very demanding test for statistical quality, much less cryptographic quality, but it is a test any CSPRNG should pass.

Diehard is useless to check the security of a CSPRNG. Cryptanalysis by experts has no substitute.
A Linear Feedback Shift Register has handsome results with Diehard -- and using it unaltered without Non-linear combination for cryptography is immediate failure with modern processing power.

https://www.wisdom.weizmann.ac.il/~oded/foc-vol1.html

Chapter 3: Pseudorandom Generators

 

[Fra93]

I compared the two with Dieharder running all the tests. Attached the results ( res.txt ), the code ( nlprg16.c and the lfsr16.c ) and the produced sequences ( nlprg.txt, lfsr.txt ).


I agree with you that shift registers-based pseudo random generators are not secure ( both the NLPRG and the LFSR ) , since there are shifts in the transfer function, ( bits that you do not need to compute in order to predict their value ). If all the bits needs to be computed ( are the output of a gate ), the problem to predict the sequence becomes cubic with the number of bits. You need to solve a system of linear equations with algorithms such as Gaussian elimination, which is still trivial as you said with modern processing power.

Having said that, the question I am trying to answer is:

Is the NLPRG more secure than LFSR? ( do you need more numbers to predict the sequence )
Has the NLPRG better statistical properties when compared LFSR? ( for instance the period of the NLPRG is one number longer than the LFSR )
etc...

If the answer is yes, than it is an improvement. Since LFSR are studied in universities, widely used in a variety of applications ( cryptography included ) and they have not been not improved since the 50s.

I do not understand much about those tests. The NLPRG has passed as assessment in all the tests except 2 weak, wheres the LFSR has passed as assessment in all the tests except 3 weak. The tests where the NLPRG and LFSR are weak are not the same.

 

[nsaspook]

Why do you have weaks. It could be anything from Bad Luck to Bad Data to Bad PRG. It still says little about how attack resistant it is.

dd if=/dev/urandom | pv | dieharder -g 200 -a
On my Linux system passes all tests with a few weaks.
https://en.wikipedia.org/wiki//dev/random#Linux
https://en.wikipedia.org/wiki/Salsa20#ChaCha_variant

Every CSPRNG should withstand "state compromise extensions". In the event that part or all of its state has been revealed (or guessed correctly), it should be impossible to reconstruct the stream of random numbers prior to the revelation. Additionally, if there is an entropy input while running, it should be infeasible to use knowledge of the input's state to predict future conditions of the CSPRNG state. Example: If the CSPRNG under consideration produces output by computing bits of π in sequence, starting from some unknown point in the binary expansion, it may well satisfy the next-bit test and thus be statistically random, as π appears to be a random sequence. (This would be guaranteed if π is a normal number, for example.) However, this algorithm is not cryptographically secure; an attacker who determines which bit of pi (i.e. the state of the algorithm) is currently in use will be able to calculate all preceding bits as well.

In practice, the output from many common PRNGs exhibit artifacts which cause them to fail statistical pattern detection tests. These include: • Shorter than expected periods for some seed states (such seed states may be called 'weak' in this context); • Lack of uniformity of distribution for large amounts of generated numbers; • Correlation of successive values; • Poor dimensional distribution of the output sequence; • The distances between where certain values occur are distributed differently from those in a random sequence distribution.

Defects exhibited by flawed PRNGs range from unnoticeable (and unknown) to very obvious. An example was the RANDU random number algorithm used for decades on mainframe computers. It was seriously flawed,[clarification needed] but its inadequacy went undetected for a very long time. In many fields, much research work of that period which relied on random selection or on Monte Carlo style simulations, or in other ways, is less reliable than it might have been as a result.

https://www.uobabylon.edu.iq/eprints/paper_1_17913_649.pdf

Good luck but I think ultimately you will agree with John von Neumann.
"Anyone who considers arithmetical methods of producing random digits is, of course, in a state of sin."

 

[unclejed613]

It produces a complete sequence.

i would ask a crypto analyst first what the ramifications of that could be... it could as easily weaken the key as strengthen it.

This slightly more secure approach might be worth the power budget.

a lot of crypto can be more easily broken by "reading" the EMI radiation from a computer's power supply, than by predicting the sequence or finding holes in the crypto method.

PRNGs are all (as a scientist from Bletchley Park noted when working on breaking the Lorentz system, which used dual PRNG cypher streams) "more Pseudo, than Random". deterministic machines can not generate truly random keys, they can only approximate randomness... for a truly unbreakable cipher, it's better to generate a key from a natural source, such as thermal/optical noise from the sun and have some way of distributing that key to both ends of the link, and use it as a one-time pad. repetition of any kind is the worst enemy of any cipher.

 

[unclejed613]

to give you an idea how repetition can expose a cryptosystem, there were two examples one from efforts to break the Enigma machine, the other from attempts at breaking the Lorentz machine.... there was a woman working on an Enigma message by hand, and Alan Turing was walking by, and glanced down at the ciphertext, and said "there aren't any "D"s in the ciphertext." as it turned out, it was part of an effort to keep up the same volume of traffic to defeat traffic analysis, and the operator had just typed "DDDDDDDDDDDD..." for the whole dummy message, which made making that day's keysettings very easy to figure out.... the second example was a Lorentz message that was over 4000 characters long (why the sender didn't put it on paper tape is unknown), and after it was sent, the recipient sent back "sorry didn't get that, send again please... so the sender reset his wheels, and typed the message again, making small changes in some places (abbreviations, etc) so that much was repetition and some of it was different, and sent with exactly the same start position for the wheels, and that was not only enough to allow the plain text to be worked out mathematically, but both key streams as well.... if it had been sent from a paper tape, or sent from where the wheels were at AFTER the first message instead, there would have been no clues given away. it also enabled the analysts to sketch out a basic diagram of how the Lorentz machine worked, and build a functional duplicate of it without ever having seen one.
it seems to me you're looking to have a keyspace from 00000 to 10000 (instead of 0000 to FFFF)... it's very likely having the two instances of 0000 is going to create a repetition, since you are encrypting bytes, and the bit for 65536 is only overflow. that condition might very well weaken your key

 

[BobW]

"there aren't any "D"s in the ciphertext." as it turned out, it was part of an effort to keep up the same volume of traffic to defeat traffic analysis, and the operator had just typed "DDDDDDDDDDDD..."

Yes. That was the fundamental flaw in the modified Enigma. A ciphertext letter could never be the same as its plaintext letter. The Polish mathematicians who were responsible for the initial cryptanalysis work on Enigma had already used that bit of knowledge towards cracking it. Ironically, this flaw came about when the Germans added a reflection rotor to the Enigma with the intention of making it more secure.

 

[Fra93]

Unclejed13 said:
it seems to me you're looking to have a keyspace from 00000 to 10000 (instead of 0000 to FFFF)... it's very likely having the two instances of 0000 is going to create a repetition, since you are encrypting bytes, and the bit for 65536 is only overflow. that condition might very well weaken your key

The sequences are complete no opinions there, for instance the 16 bits nlprg has all the numbers from 0x0000 to 0xFFFF. And I do not get what do you mean by overflow, it is a shift register and therefore there is no overflow.

You are welcome to run the code and test the produced sequences. I did not say this before but I am very happy and ready to help if anybody wants a more clear explanation of the algorithm or if somebody has problems to run the code. The best way to reach me is by email: fd at francescodellanna dot xyz.

The code is at this link https://gitlab.com/francescodellanna/nlprg/-/tree/master/examples

I tested all the nlprg sequences with a counter. For example in the 16 bits case, both of them are initialized with 0x0000, any number would work. If the counter or the nlprg reache the number 0x0000, than end the simulation. If at the end of the simulation, both the counter and the nlprg are in the 0x0000 state than the sequence of the nlprg is complete.

I explained also how it works, it is like a more complex lfsr with a sequence of 2^n-1 with a number detector and a way to insert the missing number in the sequence.

If you want to know how visit:
**broken link removed**

 

[unclejed613]

any number would work.

no matter where in the sequence you seed, the sequence remains the same, all you are doing by seeding a number is changing your start location in the sequence. for instance if you seed A2F7, and the next numbers are D17B, E8BD,F45E, and 7A2F, this is in a particular part of the sequence, so even if you started at 0000, once you get to the location in the sequence where A2F7 is, the next numbers will always be D17B, E8Bd, F45E, and 7A2F... you might as well store the whole sequence in an eprom and step through it incrementally. plus you want to add a 17th bit that is only used once, which is a waste of that bit. it would be better if you used that bit to double the length of the keyspace rather than satisfying some desire for "neatness". there may be a perfectly good reason sequences of 2^n aren't used, especially as this type or PRNG has been in use for a very long time, my guess that it would be because 2^n sequences have serious weaknesses cryptographically, otherwise 2^n-1 sequences wouldn't be so widely used as would 2^n sequences. it only takes tiny differences in the math to change a secure cryptosystem into one that leaks like a sieve...

 

[Fra93]

The 17th bit? I do not understand where does it come from, and why you bring it up. I do not want to add any extra register. All the circuits I posted before do not have extra registers.

I can post here the C code implementation of the nlprg algorithm, probably will clarify something. You are strongly encouraged to try it out.

As you see the nlprg16 function does not have any variable inside, it just shuffles the bits.
The only variable used ( nlprg ) in the main function is declared as uint16_t so 16 bits.

# include <stdint.h>
# include <stdio.h>

# define SEED 0xA013 // any seed can work

// bijective pseudo-random funcion
uint16_t nlprg16 ( uint16_t num )
{
    return
        (
        (((~ ( num >> 15 ) ^ ( num >> 14 ) ^ ( num >> 5 ) ) & 0x0001 ) << 0 ) ^ // xnor stopper
        (((  ( num >> 13 ) ^ ( num >> 12 ) ^ ( num >> 0 ) ) & 0x0001 ) << 1 ) ^
        (((  ( num >> 11 ) ^ ( num >> 10 ) ^ ( num >> 1 ) ) & 0x0001 ) << 2 ) ^
        (((  ( num >> 9  ) ^ ( num >> 8  ) ^ ( num >> 2 ) ) & 0x0001 ) << 3 ) ^
        (((  ( num >> 7  ) ^ ( num >> 6  ) ^ ( num >> 3 ) ) & 0x0001 ) << 4 ) ^
        (((~ ( num >> 5  ) ^ ( num >> 4  )                ) & 0x0001 ) << 5 ) ^ // closure connection
        //(((~ ( num >> 7  ) ^ ( num >> 4  )                ) & 0x0001 ) << 5 ) ^ // alternative closure connection #1
        //(((~ ( num >> 13 ) ^ ( num >> 4  )                ) & 0x0001 ) << 5 ) ^ // alternative closure connection #2
        (((  ( num == 0x001F ) | ( num == 0x000F )        ) & 0x0001 ) << 5 ) ^ // insert missing code 0x0031
        (( num & 0xFFE0) << 1 ) // shift for all the other bits
        ) ;

}

// used to hide the 0x000F -> 0x001F -> 0x003F transition
uint16_t shuffle ( uint16_t num )
{
    return
        (
        ((( num >> 15 ) & 0x0001 ) << 5  ) ^
        ((( num >> 14 ) & 0x0001 ) << 8  ) ^
        ((( num >> 13 ) & 0x0001 ) << 15 ) ^
        ((( num >> 12 ) & 0x0001 ) << 10 ) ^
        ((( num >> 11 ) & 0x0001 ) << 9  ) ^
        ((( num >> 10 ) & 0x0001 ) << 12 ) ^
        ((( num >> 9  ) & 0x0001 ) << 13 ) ^
        ((( num >> 8  ) & 0x0001 ) << 6  ) ^
        ((( num >> 7  ) & 0x0001 ) << 11 ) ^
        ((( num >> 6  ) & 0x0001 ) << 0  ) ^
        ((( num >> 5  ) & 0x0001 ) << 2  ) ^
        ((( num >> 4  ) & 0x0001 ) << 14 ) ^
        ((( num >> 3  ) & 0x0001 ) << 1  ) ^
        ((( num >> 2  ) & 0x0001 ) << 4  ) ^
        ((( num >> 1  ) & 0x0001 ) << 3  ) ^
        ((( num >> 0  ) & 0x0001 ) << 7  )
        );

}

// testbench for the non-linear pseudo-random generator
int main ()
{

    uint16_t nlprg   = SEED ;
    int      period  = 0    ;
    int      verbose = 1    ;
    

    if ( verbose ) printf ("type: d\ncount: 65536\nnumbit: 16\n");

    do {

        nlprg = nlprg16 ( nlprg ) ;
        period ++ ;

        //if ( verbose ) printf ("period %6d   nlprg %6d\n", period, shuffle ( nlprg ) );
        if ( verbose ) printf ("%6d\n", shuffle(nlprg)  );

    } while ( nlprg != SEED ) ;

  return 0 ;

}

The truth is that 2^n pseudo-random sequences generated by "shift registers" did not exist in the past and 2^n-1 are good enough.

Besides you can store 2^16 numbers in a EPROM ( it is a waste for a good memory ), but you can not store 2^256 bits.

 

[unclejed613]

but you can not store 2^256 bits.

but you don't have that many bits in the keystream, you have 65536 long integers, which is only a stream of 1048576 bits, and then the pattern repeats...

to get 2^256 bits of keyspace, you need 256 shift elements and the accompanying gates...

 

[Fra93]

I show how to create those sequences, the nlprg algorithm can scale.

I in a previous post examples ranging from 3 to 16 bits. https://www.electro-tech-online.com...mplete-numerical-sequence.158989/post-1377868

Nothing limits the bit length.

I do not have a 256 bit example to share here, but it is theoretically possible to create one. I do not have the computational resources to test one.

 

[rjenkinsgb]

Firstly, I freely admit I have no knowledge of the cryptography implications.

However, to me this all seems a long way around what looks to be a trivially simple problem:
Why not just use a longer conventional PRNG but only take a small number of bits from that, for whatever size is needed?
eg. a 64 bit (or larger) PNRG to give 16 bit output values & so on.

Won't that then give a complete set of 16 bit values and also be far harder to derive the overall sequence, than using (and in effect revealing) the full bit size of the PRNG?

Without actually writing anything to test it, it appears a conventional xor feedback type of a much larger size would be computationally faster than the algorithm you suggest, with all the convoluted tests and bit manipulation?