Power Electronics - Bridge Rectifiers

[Oranje]

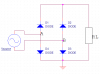
Good Day Experts,

I am studying single phase uncontrolled rectifier bridge. One thing that I am confused about is whether the fundamental component of voltage and current (as well as non-fundamental component) are both an inherent property of the ac source, certain connected load, or both the ac source and the load? Is it true that in my duplex residential receptacle (120Vrms ~ 170Vpeak) there is also this presence of fundamental component and non-fundamental component? In my understanding, the source is a sinusoidal function which can be broken down into sum of infinitely many terms. The greater quantity of terms you sum, the better the approximation to the original sinusoidal function. Please confirm if my calculation of fundamental component of source current is correct. If it is, what does f(x) represent in equation below?



\[f(x)=\sum_{n=1}^{inf}b_{n}sin(nx)dx\]

\[b_{1}=\frac{2}{\pi}\int_{0}^{\pi}f(x)sin(nx)dx\]

\[b_{1}=\frac{2}{\pi}\int_{0}^{\pi}I_{0}sin(\omega t)d\omega t= -\frac{2I_{0}}{\pi}cos(\omega t )\mid _{0}^{\pi}=\frac{4I_{0}}{\pi}\]

 

[Oranje]

Can anyone help out with this question?

 

[crutschow]

The source generator is sinusoidal.
The loads are what can cause phase-shift and distortion of the current waveform as compared to the voltage waveform.
The distorted current can cause distortion in the voltage waveform due to line and generator impedance.

In my understanding, the source is a sinusoidal function which can be broken down into sum of infinitely many terms.

A pure sinusoid can't be broken down any further.
A distorted or non-sinusoidal waveform can be separated into a series of sinusoidal functions (Fourier transform).

 

[Oranje]

Thank you for your reply. So is it true that if the load consists of a highly inductive load (RL), the load distorts the pure sinusoid and load current can be broken down into Fourier series representation? However, if we connect a purely resistive load (R), Fourier series representation is not possible? I have also attached a circuit representation to help us.

 

[crutschow]

Thank you for your reply. So is it true that if the load consists of a highly inductive load (RL), the load distorts the pure sinusoid and load current can be broken down into Fourier series representation? However, if we connect a purely resistive load (R), Fourier series representation is not possible? I have also attached a circuit representation to help us.
View attachment 118354

The diode bridge can distort the current waveform, depending upon the load.
For example the capacitive filter of a typical AC-DC supply can cause high peak currents near the peak of the AC waveform.
The inductance is only a factor in that if it's in the AC side of the load, not the DC side.

A pure resistive load driven by a sinusoid can be represented by a Fourier series, but there is only one element in the series.

 

[Oranje]

Let us work via an example below (ckt attached below). This example came from nptel lecture series (Lecture 13) by Professor Fernandes of Bombay University.
Problem Content: Triggering angle is maintained at 110 degrees. Current becomes zero at 50 degrees beyond the zero crossing of the positive half cycle. Sketch the load current and applied average voltage waveform. Find the average output voltage.

Givens: Iavg. = 1.8Adc, R = 6 ohm.

Notes from Professor:
<SCR, T1, is triggered at ωt=110° or 11π/18
<At ωt=230° or π+π/18 or 50° passed the zero crossing, current becomes zero.
<Remember, as long as SCR conducts, output voltage follows the input voltage.
<Output voltage follows the input voltage from ωt=110° to ωt=180°
<From ωt=180° to ωt=230° free-wheeling diodes are conducting. At ωt=180°^+, the potential of point B is higher than potential of point A. This means T1 turns off and D3 starts conducting. Until T4 is triggered, current free-wheels through D3 and D2.
<Output voltage from ωt=180° to ωt=230° is zero.
<At ωt=230° current dies down and reaches zero.
<From ωt=230° to ωt=110°+180°=290° output voltage is equal to E.
<<If we had an RLE load, output voltage would be zero and not E.
<Source current is same as the load current in the powering mode (T1 and D2 conduct) and when (D3 and T4 conduct).
<At ωt=180°^+, T1 turns off and if we assume source inductance to be zero, immediately source current becomes zero.

Going Back to My Initial Question:
Since load is not highly inductive, load current is discontinuous. This non-sinusoidal function may be approximated via Fourier Series representation? Likewise, because output voltage function is non-sinusoidal it, also, may be approximated via Fourier Series? Please correct me if I'm wrong.
Based on lecture, inductance on load side plays a huge, very important role. Is this true, or should I change the source of where I get my lectures? Please let me know.