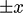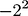Order of Operations Conventions

[jpanhalt]

This thread has been split off from the following thread:
https://www.electro-tech-online.com/threads/how-do-i-in-latex.147332/

As I recall, -2^2 = -4 by today's conventions. You seem to be missing a parenthesis or two. So, perhaps to be consistent, the roots should be 2 and (-2). I hope that seminal thread has not been lost. I learned a lot from it.

John

 

[DerStrom8]

As I recall, -2^2 = -4 by today's conventions. You seem to be missing a parenthesis or two. So, perhaps to be consistent, the roots should be 2 and (-2). I hope that seminal thread has not been lost. I learned a lot from it.

John

Hmm, fair point I suppose, though generally I think

implies (+x) and (-x). You really only need the parentheses if you are going the other way around, squaring the value.

 

[jpanhalt]

That is what Papabravo and I both thought, and it was was taught that way at least through the 1970's. Don't know when the change occurred. But, you have to roll with the punches, so long as they are consistent. Frankly, [latex]-2^{2}=4[/latex] never caused a problem until some pedagogue decided it did.

I think

implies (+x) and (-x). You really only need the parentheses if you are going the other way around, squaring the value.

Not really. If you don't happen to know the alternate code for ±, then you have to write +2 and -2. The parentheses are not implied in the strictest sense. One must be consistent. Now, one might accept (±2), but that is not what you wrote. Don't get me wrong. I think the change is silly.

John

 

[DerStrom8]

equals -4 due to PEMDAS. Exponents come first, addition/subtraction/negation last. That's why I said it's important to use parentheses when you're going the other way around. When you're squaring a negative value the parentheses are absolutely necessary. But when you're taking the square root you do not need parentheses, the answer is simply ±x

 

[large_ghostman]

Today your told to drop parenthesis where you can, not too sure of the reasoning for this. Thanks for all the heads up i will have a try .

 

[djsfantasi]

That is what Papabravo and I both thought, and it was was taught that way at least through the 1970's. Don't know when the change occurred. But, you have to roll with the punches, so long as they are consistent. Frankly, [latex]-2^{2}=4[/latex] never caused a problem until some pedagogue decided it did.


Not really. If you don't happen to know the alternate code for ±, then you have to write +2 and -2. The parentheses are not implied in the strictest sense. One must be consistent. Now, one might accept (±2), but that is not what you wrote. Don't get me wrong. I think the change is silly.

John

There are different conventions regarding unary operations. In particular written mathematics convention is that -2^2=-4. However, in coding, the unary operator has precedence over the binary (2 operands, not base2) operators. Hence -2^2=(-2)^2.

 

[Pommie]

Minus 2 squared has always, and always will be, 4. End of.

Mike.

 

[DerStrom8]

Minus 2 squared has always, and always will be, 4. End of.

Mike.

Only if "minus 2" is defined as "-2" with parentheses. Once again, use the order of operations (PEMDAS).

 

[Pommie]

Minus 2 times minus 2 is 4. Simples.

Mike.
P.S. stick it in your calculator and see what it thinks.

 

[large_ghostman]

both mine say 4 although one dosnt like me starting with a -2 !!!! I will try on the graph calculator as well it would be interesting to see if ANY come up with a different answer as most are now VEPRAM or equivalent

 

[large_ghostman]

Graph says 4. EXCEL on the other hand says -4!! So does Matlab, so as AUS Dave would say 'A trap for young players!'.
Interesting stuff!

 

[KeepItSimpleStupid]

matt:

Usually you can do a quote and get back the Latex. On this thread, there's too much of mix of pics and real Latex and I tried it on a few posts in this thread and got image results.

 

[Pommie]

EXCEL on the other hand says -4!! So does Matlab

Excel (2013) says 4, I put in =-2^2.

Mike.

 

[large_ghostman]

Excel (2013) says 4, I put in =-2^2.

Mike.

I did it wrong then Pommie, I put -2+-2= doing what you did gave me 4 in both Matlab and excel as well, sorry for the mess up everyone

 

[DerStrom8]

I did it wrong then Pommie, I put -2+-2= doing what you did gave me 4 in both Matlab and excel as well, sorry for the mess up everyone

I think you mean -2*-2?

 

[jpanhalt]

I may have confused Pommie with Papabravo in the much earlier thread I recollected. If I did, please accept my apology. Anyway, I couldn't find that thread. At the time, I made some comment to the effect that negative numbers might be considered as entities themselves, rather than as "-1 x number." My concern was that application of PEMDAS in that way effectively eliminates "negative" numbers. In other words, I support the view that we have "negative numbers," and we have negation as an operator.

Yesterday, I did find a discussion from Drexel University that I had previously missed on the very point of PEMDAS as applied to negative numbers. My reading of that essay is that the matter is not completely settled (https://mathforum.org/library/drmath/view/61633.html ).

Can someone here provide a more current and definitive statement on the subject?

John

 

[large_ghostman]

No I meant -4 Matt :S

 

[DerStrom8]

I have always seen -x treated as 0-x, in which case negation is a form of subtraction and thus is completed last. I haven't looked for any definitive articles on the subject though.

 

[DerStrom8]

The gentleman who wrote in the link John posted seems to agree with me in a different post:



Also, regarding Excel, notice the last paragraph on the page:

You may be interested in this page I ran across, on the order of
operations in Microsoft Excel. It says that they evaluate unary minus
before exponentiation, and will not change it though they acknowledge
that this is different from the normal order

Microsoft understands that their "order of operations" is not standard, but still refuses to change it. For that reason I don't put much trust in what is returned from Excel.

 

[large_ghostman]

The gentleman who wrote in the link John posted seems to agree with me in a different post:



Also, regarding Excel, notice the last paragraph on the page:



Microsoft understands that their "order of operations" is not standard, but still refuses to change it. For that reason I don't put much trust in what is returned from Excel.

Considering excel is supposed to be 'THE' spreadsheet, why would they do something that stupid??? That is totally bonkers. I wonder if open office blindly followed them