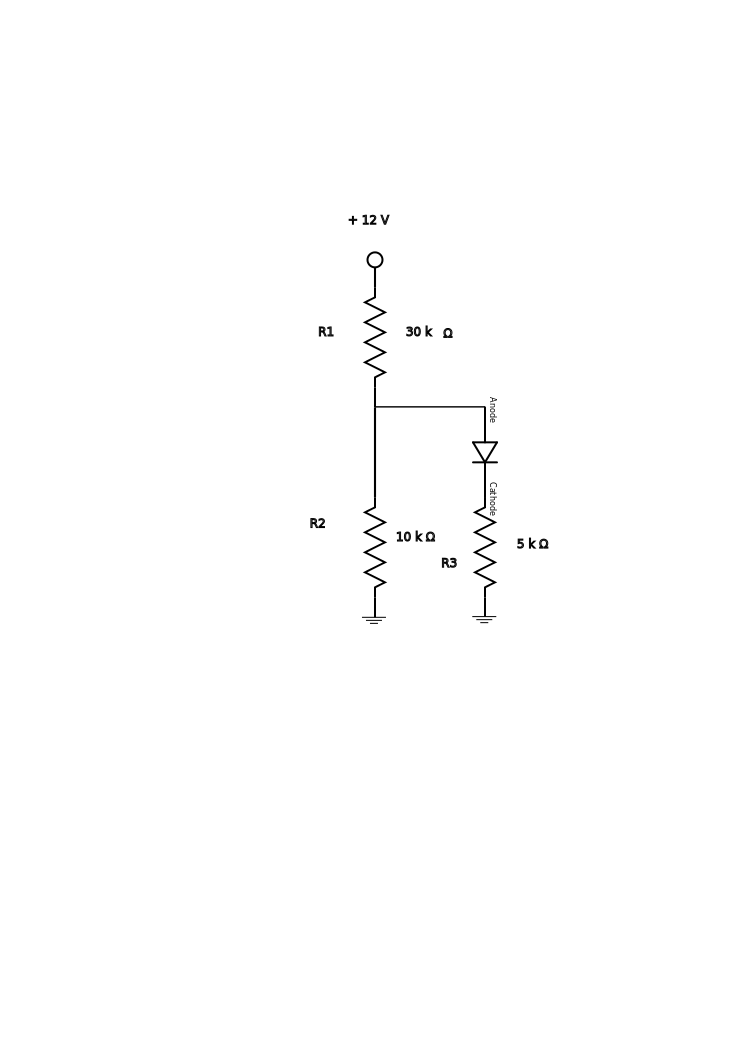
Hello there,
To the OP:
The simplest method to use here to calculate the required currents and/or voltages is to simply replace the diode with a voltage source which is approximately equal to the diode voltage drop when it is passing a current of the required current. Assuming this is a regular rectifier diode, the assumed value is usually 0.7 volts. So you would remove the diode, and replace it with a battery (positive terminal goes to the 'anode' connection, negative terminal to the 'cathode' connection) of 0.7 volts. You would then analyze the circuit just like any other two source circuit.
If you happen to have the curve for the diode (we dont always have this information anyway) you can use that to 'upgrade' the analysis using an ad hoc method of approximation that involves changing the assumed voltage drop (the battery) and recalculating, then repeating until you get the desired accuracy. But the temperature also affects the diode voltage drop so we often just use a first approximation and let it go at that. But if you already know the diode current you're one step ahead because you can look at the diode curve and find the voltage (which will be approximate anyway) and then use that in the calculations. Since you know the diode current is 0.25 milliamps, you're one step ahead of the game already.
You could also build up an equation that includes the diode curve, but i assume you dont want to have to go through all that. So start with the assumed voltage drop of 0.7v and see what you can do with it. If you need help with a two source circuit that's not a problem either.
If you'd like to check your result, you can use this formula for the diode current:
i=(Vs*R2-Vd*R2-Vd*R1)/(R2*R3+R1*R3+R1*R2)
where
Vs is the source voltage (12v here),
Vd is the diode voltage (we said we would assume is 0.7v),
i is the current through the diode (you said would be 0.000250 amps here),
R1 through R3 are the resistors.
You would plug in all the values and compute the result to check your own result.
You could 'cheat' and solve that equation for R2, but you should try to develop a solution yourself first