How can one calculate an angle of a circular logarithmic scale?

[Rich D.]

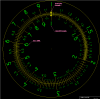
Easiest way for my brain to explain the question is with this ugly, ugly drawing.

I would like to know where to draw the 2, 3, 4...etc around a circular scale with the 1 and/or 10 at the top position.
For example, how many degrees is the 2?
I'm looking for a formula where I plug in the number (from 1.0 to 9.999) and get a positive angle from the top 12:00 position.

The end goal is to print out a scales to make analog computers - or - a circular slide rule.

 

[jpanhalt]

What sort of precision do you need? A simple table may suffice. Is this for the 24F chip?

I have used circular slide rules many times, circa 1968 for navigation.

 

[Rich D.]

No electronics involved beyond a CAD program. I am attempting to draw some scales and print them and mount them the way it used to be done. On the printer, a precision of single digits of a degree would be good enough for a 5" wheel.

 

[JimB]

The angle is given by the following:

Angle = 360 * Log(Number)

Where
Angle = the number of degrees past the 12 o'clock position
Number = the number you want to put on the scale
Log = logarithms to base 10

JimB

 

[Rich D.]

Thanks JimB...That works perfectly. I knew I had to throw a log in there somewhere but couldn't get my head around it.

 

[JimB]

Success, love it!

JimB

 

[dknguyen]

Magical.

 

[Rich D.]

Still tediously adding in all the lines but this gives any reader here what this project is about.

 

[atferrari]

Out of curiosity Rich

In your process, nothing happens below 1?

 

[Rich D.]

It's an analog calculator with a logarithmic scale for multiplication and division. There is no 0, going clockwise, it continues infinitely to 10, 100, 1000... and going counter clockwise it becomes 0.1, 0.01, 0.001, 0.0001... For multiplication and division, zero is not really needed, since anything x0 is 0. And as you can deduce from a calculator, dividing by zero causes an error. That's how slide rules are made...you know...the thing engineers used to get us to the moon and back before they could afford desktop PCs. The C and D scales do not have a zero.

In this particular application for music, I will be computing beats per minute, beats per second, and milliseconds per beat, and related calculations so zero would not apply as that would be silence. I already made a linear one that computes millisecond additions and subtractions and it's calibrated in the form of note lengths (quarter note, 8th note triplets...). This one needed a log scale to multiply and divide. I will mostly use it to calculate milliseconds of delay for particular tempos. Right now I use a chart full of numbers. It is a bit cumbersome and usually leaves me cross-eyed with its vast array of numbers. Even then I have to interpolate between entries.

 

[atferrari]

By the time I became somewhat profficient with it, electronic calculators took over.

 

[JimB]

In your process, nothing happens below 1?

For multiplication and division, zero is not really needed, since anything x0 is 0. And as you can deduce from a calculator, dividing by zero causes an error.

In the mathematical world, Log (0) is undefined, it just does not exist.

JimB
(Skating on thin ice at the edge of his mathematical knowledge!)

 

[Musicmanager]

<<<<<<<<<<<<<<<<< Musician, NOT Mathematician !!


Not doubting you in the slightest, but very confused ... .. ..

What do you call a point exactly half way between 1 and -1 then ??

S

 

[JimB]

What do you call a point exactly half way between 1 and -1 then ??

Zero.

But Log(0) does not exist. (As far as I know).

Logs only exist for numbers greater than 0.

JimB

 

[Musicmanager]

If the explanation I've just read on Google has got through to me .. .. it's because a log is a multiplication and anything times 0(zero) is 0(zero)

I think I'll just go back to sleep, my head hurts already !!

S

 

[JimB]

I think I'll just go back to sleep, my head hurts already !!

a good scheme!
JimB

 

[Rich D.]

< Musician, NOT Mathematician !!

In the music world, a tempo of zero does not exist, nor does a 1/4096th note. Even gain knobs don't really go down to zero, they just go to negative infinity. (They can go to 11 though, as described by the Tufnel theorem.)
As a musician, you know that zero exists, you just don't use it in music conversation so much. It more likely exists in your bank account.
Zero both exists and doesn't exist depending on the world you are in... sorta' like some would say about God, no?

 

[Rich D.]

For any nerds interested, here is the finished result. How to use? Print out two copies, cut out the inner circle on one, and attach the two center pivot points with a screw or something.
If the pivot point is set well, with interpolation you can figure on about 3 significant digits of precision.

To use, set the inner '6' to the tempo in BPM (beats-per-minute), and read the delay time for an effect processor at the outer '1' index mark. (For example, setting the inner '6' to 90 BPM, it would line up at .666 seconds.)
These kinds of computers can't figure out the decimal range though, you would have to just know from basic intuition that the 6.66 mark isn't 66 seconds or 6.6 seconds or 0.066 seconds.
Since the '6' point is used for calculating 1/4-note beats, you can use the '3' for 1/8-note beats, 1.5 for 1/16-note beats, etc. or to save a bit of time, 8th notes can be read from the outer '5' instead of the outer '1' index, 16th notes from the '2.5' index, and so on.

It's all very fun for nerds.

And BTW: This can be adapted very easily for ohms law, voltage = current x resistance, or the other formula watts = voltage * current, and I suppose a lot of other simple multiply or divide calculations in electronics.

If anybody is crazy enough to want one, let me know and I can provide a high-resolution PDF or something with a white background. This example JPG isn't really good for printing.

 

[unclejed613]

In the music world, a tempo of zero does not exist, nor does a 1/4096th note. Even gain knobs don't really go down to zero, they just go to negative infinity. (They can go to 11 though, as described by the Tufnel theorem.)

 

[Rich D.]

...yea, what he said. 11 is louder than 10 because it's one more. 10 just can't be as loud, it's just not possible.