How to calculate the value of a smoothing capacitor

[MrAl]

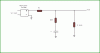
We should all be using the same circuit, same frequency, and calculate the percent ripple on the same reference (peak DC voltage or average DC voltage).

Tony was using loads of 100 ohms and 10 ohms; why are you using 13 ohms?

Please post the circuit you're using and list all the relevant details; tell what you change from experiment to experiment.

Hi again,

Sorry about that, i meant to mention that i changed from 100 and 10 ohm loads to 130 and 13 ohm loads. The reason for this was i was using 100vrms input, which was giving me a DC voltage in the ballpark of around 130 or so volts, and i wanted to get 1 amp for the initial experiment, so i went with 130 ohms. This doesnt give me exactly 1 amp, but it's around that area.

I could change back to 100 ohms and 10 ohms, and adjust input to get 1 amp and about 10 amps.

With 74vac rms input i get close to 100v output, so now i use 100 ohms and 10 ohms again, and 60Hz but could change to 50Hz if you like. I also use Rs=0.1 ohms, the resistor from the output of the bridge rectifier to the cap. So the circuit is just a bridge rectifier with cap, load resistor, cap ESR, and series Rs between bridge and cap ESR and output.

So listing in order all except Rs as Rs=0.1 always, we have:
Table organization: RLoad, C, CapESR, PercentRipple
Table:
100, 2000uf, 0.00, 3.6%
100, 2000uf, 0.15, 5.1%
10.0, 2000uf, 0.15, 28.3%
10.0, 20000uf, 0.15, 14.7%
10.0, 20000uf, 0.015, 3.4%
and just for kicks:
10.0, 200000uf, 0.15, 13.9%

Note two main things:
The first and last percent ripple in the main table both come out close to 3.5 percent.
The last line after that comes out to 13.9 percent, even after increasing the cap
value another 10 times to 200000uf. So the only way to get back to 3.5 percent
was to decrease the ESR of the cap.
This is easily explained by noting that the cap itself becomes an almost constant DC source, so the ESR acts as an AC voltage divider (biased with DC) which places AC at the output, and there is no way to get rid of that effect through any means other than lowering the ESR. So at some point the ESR becomes a problem for meeting the required ripple voltage spec. This also means that the wiring resistance to and from the cap has to be considered carefully as well.
Just to note, decreasing the ESR to 0.062 got me back to 5.1 percent ripple with the heavier load.

When i worked in the industry, we used screw top capacitors and thick copper buss bars to connect several capacitors in parallel.

 

[Tony Stewart]

Conrad Hoffman pointed this out some years ago. This is a fact worth noting. The best DF is typically to be found in the 50 to 100 volt range. He especially has noted that very low voltage electrolytics, such as 6.3 or 10 volts seem to be more failure prone.

I dont know CH but it seems we share a common interest in observing geometric ratios.

My Test Eng experience from lots of fragility testing on disk drives and HDD cartridges, used vel. vs. accel damage boundary curves resulted in my observation that mechanical shock level can be approximated easily from drop and stop height. .i.e. if any mass drops freefall from height , h and stops in depth, d , due to some uniform compression material, the linear ratio h/d=N , the number of g's of shock. Free fall amusement rides from h that curve to horizontal stop in same distance are constant g but rotating vector. A Glass object that falls from 1m but only compresses 1mm will experience 1000 g's. Thus packing foam density depends on weight but g levels are designed for 1m drop from truck and stop travel inside. However damage criteria depends on Inertial momentum and breakdown threshold and thus mass x velocity. But in estimating g levels, it can always be estimated by h/d ratio due to gravity.

I use the same analogy for ESR ratios between source and load for load V regulation% and %power dissipation between source and load sharing the same current, analogous to gravity.

 

[Tony Stewart]

Good points MrAl.
I think the reason dissipation factor was increased 2% per mF above 1mF in SMT caps , that I examined was increasing difficulty of maintaining same X/R impedance ratios in small geometry parts at 120Hz . But given no limits on size, it would be possible to maintain this.

The other issue is lifespan of all current ripple caps is short and rated by different temps. Vs time e.g. @3000h, then ESR losses cause temp rise which degrades life by Arrhenius law for all chemistry E.g. 2x per 10 -15 degC reduction towards room temp. or conversely 50% reduction for every 10-15 deg rise. Given dielectric is also a thermal insulator, the conductor geometry dictates thermal rise and maximum ripple current, which must be factored with reliability as ESR rises over time with degradation , so safety derating factors must be considered for reaching expected life, often the weakest link in any good power supply design.

 

[The Electrician]

So listing in order all except Rs as Rs=0.1 always, we have:
Table organization: RLoad, C, CapESR, PercentRipple
Table:
100, 2000uf, 0.00, 3.6%
100, 2000uf, 0.15, 5.1%
10.0, 2000uf, 0.15, 28.3%
10.0, 20000uf, 0.15, 14.7%
10.0, 20000uf, 0.015, 3.4%
and just for kicks:
10.0, 200000uf, 0.15, 13.9%

My simulation use a different model for the diodes, so I don't get exactly what you do, but I get essentially the same.

These results are what one could expect without resorting to full analysis.

The ripple voltage is determined primarily by the voltage drop of the ripple current across the series connection of the two components making up the impedance of the capacitor, namely the reactance of the capacitance and the ESR. If one of these components dominates, the ripple voltage will be mostly determined by that component's impedance, and making the other component even smaller certainly won't help much.

With a 2000 uF cap, its reactance is .663 ohms (at 60 Hz). Connect that in series with .15 ohms ESR, and we have a capacitor with a DF (dissipation factor) of .226 which is not too much for a non-defective aluminum electrolytic capacitor of this size. The ripple voltage for this cap isn't much different for an ESR of zero or of .15 ohm because the reactance of .663 ohms dominates.

Now if the capacitor is increased by a factor of 10, the reactance decreases by a factor of 10--now the reactance is .0663 ohms. This is small enough that the ESR of .15 ohms dominates, and we shouldn't be surprised that further increasing the capacitance doesn't reduce the ripple voltage--the ripple voltage is determined by the ESR. To further reduce the ripple voltage we must obviously reduce the ESR.

Note that when the cap is increased to 20000 uF with an ESR of .15 ohms, the DF becomes 2.26; this is what we would have if the capacitor were defective, so we shouldn't be surprised that if such a bad capacitor were used, the ripple voltage would be high. When I used to repair electronics, seeing a high ripple on a supply line was the first sign that the filter cap was bad.

As you pointed in an earlier post, if the capacitance is increased by connecting several of the existing capacitor in parallel, the ESR will automatically decrease in the same ratio as the capacitive reactance decreases. The DF of the composite capacitor will remain the same, and if the ESR of the single capacitor wasn't too high, then the ESR of the composite capacitor shouldn't be either.

 

[The Electrician]

I use the same analogy for ESR ratios between source and load for load V regulation% and %power dissipation between source and load sharing the same current, analogous to gravity.

I quite agree that ESR is the relevant factor in power dissipation calculations, but I don't see how ESR in non-defective aluminum electrolytics has much effect on voltage regulation (voltage ripple?) at grid frequencies. Insofar as a property of the filter cap has an effect, it's the capacitance that matters not the ESR (for a good capacitor). Certainly at the frequencies seen in SMPS applications, ESR is usually dominant, but not at grid frequencies. Perhaps you could explain further.

 

[MrAl]

My simulation use a different model for the diodes, so I don't get exactly what you do, but I get essentially the same.

These results are what one could expect without resorting to full analysis.

The ripple voltage is determined primarily by the voltage drop of the ripple current across the series connection of the two components making up the impedance of the capacitor, namely the reactance of the capacitance and the ESR. If one of these components dominates, the ripple voltage will be mostly determined by that component's impedance, and making the other component even smaller certainly won't help much.

With a 2000 uF cap, its reactance is .663 ohms (at 60 Hz). Connect that in series with .15 ohms ESR, and we have a capacitor with a DF (dissipation factor) of .226 which is not too much for a non-defective aluminum electrolytic capacitor of this size. The ripple voltage for this cap isn't much different for an ESR of zero or of .15 ohm because the reactance of .663 ohms dominates.

Now if the capacitor is increased by a factor of 10, the reactance decreases by a factor of 10--now the reactance is .0663 ohms. This is small enough that the ESR of .15 ohms dominates, and we shouldn't be surprised that further increasing the capacitance doesn't reduce the ripple voltage--the ripple voltage is determined by the ESR. To further reduce the ripple voltage we must obviously reduce the ESR.

Note that when the cap is increased to 20000 uF with an ESR of .15 ohms, the DF becomes 2.26; this is what we would have if the capacitor were defective, so we shouldn't be surprised that if such a bad capacitor were used, the ripple voltage would be high. When I used to repair electronics, seeing a high ripple on a supply line was the first sign that the filter cap was bad.

As you pointed in an earlier post, if the capacitance is increased by connecting several of the existing capacitor in parallel, the ESR will automatically decrease in the same ratio as the capacitive reactance decreases. The DF of the composite capacitor will remain the same, and if the ESR of the single capacitor wasn't too high, then the ESR of the composite capacitor shouldn't be either.

Hi,

I think it is interesting to look at the ratio of the ESR to capacitor reactance, but i dont believe it tells the whole story about the ripple. If we make a measurement and find that the ripple voltage is large compared to what we typically see, then we know the ESR probably increased and so the circuit is no longer going to function properly. But if we DONT see a ripple voltage that is higher than what we typically see, then we cant be sure if the ESR increased or not. That's because it also depends on the load, and so for some circuits the ESR can be quite high before we see any difference.

For example, a 2000uf cap with ESR=1.5 leads to a dissipation factor the same as a 20000uuf cap with ESR=0.15, yet with 1000 ohms load (using the 2000uf, 1.5R cap) we only see about 6 percent ripple, which is not high at all unless the application previously showed a much lower percentage. But if we lower the load to 100 ohms, then we immediately see a higher ripple of about 25 percent, which would be too high in most cases, and if we lower the load to 10 ohms then we see a whopping 73 percent ripple, to be a little extreme. With 10k load we see almost no ripple.

So when we go from 100 ohms to 1000 ohms we saw a decrease in ripple of almost 20 percent, all the while using the same capacitor with what seems like a large ESR.
I mention this also because caps come with a pretty wide range of ESR values, and although we might not find ones with a super high ESR, i think we still limit our view too much if we only consider the ratio of ESR to cap reactance, which does not take into account the load at all.

I guess another view is if we measure the ripple and see that it is higher than we typically see for the given application, we cant be entirely sure if the ESR increased or something happened to the load such that it is drawing more current than it usually does for that application. If we check the cap and it is bad, then that was probably it, but if it is good then the load current may have increased due to a faulty component down the line somewhere.

As a side note, i have had success testing my capacitors with a square wave through a series resistor. The ESR shows up nicely on the scope. When i fixed a few things that had bad electro's, i found that the capacitance decreased quite a bit as well as the ESR went high.

 

[Tony Stewart]

I quite agree that ESR is the relevant factor in power dissipation calculations, but I don't see how ESR in non-defective aluminum electrolytics has much effect on voltage regulation (voltage ripple?) at grid frequencies. Insofar as a property of the filter cap has an effect, it's the capacitance that matters not the ESR (for a good capacitor). Certainly at the frequencies seen in SMPS applications, ESR is usually dominant, but not at grid frequencies. Perhaps you could explain further.

The main reason electrolytics have improved over the years is due to low ESR which most important for high current SMPS. But still important for 2x grid rates, which why is they continue to spec the dissipation factor due to ESR as δ or % at 120 Hz. After all thus is the only variable that causes self-heating and degradation and reduced lifespan. As we know the most unreliable part on old electronics are the electrolytic caps.

For reliability reasons, it is better to accept more ripple voltage in order to reduce ripple current. In Mil-Std handbook 217 the failure rate multiplier for electrolytics is inversely rated with circuit ESR. Thus series R and L filters are recommended, which adds to load droop and in some dynamic cases, a 10% preload reduces the V max-min swing even though ripple voltage is reduced.

The maximum peak voltage to RMS is √2. The drop in Vavg is usually 50% of ripple Vpp from no load to,load.
This with series R + cap ESR /load ratio or load regulation error.

 

[The Electrician]

Hi,

I think it is interesting to look at the ratio of the ESR to capacitor reactance, but i dont believe it tells the whole story about the ripple.

The particular story it does tell is whether increasing the capacitance while the ESR remains fixed is going to decrease ripple; that's the issue I'm dealing with in post #144. If the ESR is larger than the reactance, then increasing the capacitance (decreasing reactance) certainly isn't going to reduce ripple. Full analysis is not needed; just look at the dissipation factor. And it doesn't matter what the load is--increasing capacitance won't decrease ripple if the DF is high and if ESR remains fixed as capacitance increases. Fortunately, however, the way capacitance is increased is either by paralleling several capacitors, or by buying a cap with larger capacitance. In both cases, ESR decreases "automatically" as capacitance increases, so ESR remains less than reactance, and therefore ESR continues to have negligible effect on ripple voltage.

The reactance should always be larger than the ESR (at two times grid frequency) in a good filter of the type we're discussing; this is a property of good capacitors. A low ESR is important for other reasons too, but it need not be extremely low to get low ripple; it only has to be several times less than the reactance for the capacitance to dominate the ripple voltage, which it will be in a non-defective capacitor.

The value of capacitance is what is chosen to give the desired ripple voltage without regard to ESR. ESR need not be considered when choosing a cap for desired ripple because for a good cap, ESR has little effect on ripple. ESR has an effect on internal heating of the capacitor, and should be taken into account for that reason, but it need not be considered with respect to ripple voltage for non-defective capacitors (having low DF, in other words), regardless of load.

If we make a measurement and find that the ripple voltage is large compared to what we typically see, then we know the ESR probably increased and so the circuit is no longer going to function properly.

Why would one suppose that the cause of increased ripple is increased ESR, rather than decreased capacitance?

But if we DONT see a ripple voltage that is higher than what we typically see, then we cant be sure if the ESR increased or not. That's because it also depends on the load, and so for some circuits the ESR can be quite high before we see any difference.

Ripple voltage does indeed depend on the load, even if ESR is zero.

But dependence of ripple on load isn't the major reason why we can't be sure if the ESR has increased or not.

I agree that ESR can increase quite a bit (if the capacitor is not defective to start with) before we see more ripple. The reason for this is because a properly designed filter would use non-defective capacitors to start with. For such caps, the DF is low, meaning the ESR is substantially lower than the capacitive reactance, and the ripple is not much determined by the ESR, regardless of load. If the capacitor is becoming defective, since the ESR to start with when the cap was new was much less than the capacitive reactance, it can increase quite a bit before its effect on ripple is noticeable; the ratio of ESR to reactance is telling the story here.

For example, a 2000uf cap with ESR=1.5 leads to a dissipation factor the same as a 20000uuf cap with ESR=0.15, yet with 1000 ohms load (using the 2000uf, 1.5R cap) we only see about 6 percent ripple, which is not high at all unless the application previously showed a much lower percentage. But if we lower the load to 100 ohms, then we immediately see a higher ripple of about 25 percent, which would be too high in most cases, and if we lower the load to 10 ohms then we see a whopping 73 percent ripple, to be a little extreme. With 10k load we see almost no ripple.
So when we go from 100 ohms to 1000 ohms we saw a decrease in ripple of almost 20 percent, all the while using the same capacitor with what seems like a large ESR.

I'm saying that what DF (the ratio of ESR to reactance) can tell us is whether increasing capacitance while keeping ESR constant is going to reduce ripple voltage. Your examples above are of a different scenario and they don't show that DF doesn't indicate what I describe in post #144..

I mention this also because caps come with a pretty wide range of ESR values, and although we might not find ones with a super high ESR, i think we still limit our view too much if we only consider the ratio of ESR to cap reactance, which does not take into account the load at all.

Again, the reason for considering the ratio of ESR to reactance is with respect to the question of whether increasing capacitance with a fixed ESR will reduce ripple voltage. With respect to this question, load doesn't come into it at all. There are other things to consider, but this is the only view I was considering, and with respect to it, the ratio of ESR to reactance is the relevant factor.

 

[Tony Stewart]

The ESR component of D, the dissipation factor comes to be significant simply with load regulation.

Load regulation can be simplified as a ratio of source/step-load resistance (or more accurately ESR/(ESR+RL) = % step load regulation voltage.

Thus the source ripple is increased by this ratio minimum, as well as a steady state component of ripple current, Ipp*ESR

But equally important, ESR is the only electrical parameter in the capacitor which causes heat, the prime cause of capacitor degradation, which becomes a tradeoff with desired ripple V by large peak currents with low %Vripple .

 

[MrAl]

The particular story it does tell is whether increasing the capacitance while the ESR remains fixed is going to decrease ripple; that's the issue I'm dealing with in post #144. If the ESR is larger than the reactance, then increasing the capacitance (decreasing reactance) certainly isn't going to reduce ripple. Full analysis is not needed; just look at the dissipation factor. And it doesn't matter what the load is--increasing capacitance won't decrease ripple if the DF is high and if ESR remains fixed as capacitance increases. Fortunately, however, the way capacitance is increased is either by paralleling several capacitors, or by buying a cap with larger capacitance. In both cases, ESR decreases "automatically" as capacitance increases, so ESR remains less than reactance, and therefore ESR continues to have negligible effect on ripple voltage.

The reactance should always be larger than the ESR (at two times grid frequency) in a good filter of the type we're discussing; this is a property of good capacitors. A low ESR is important for other reasons too, but it need not be extremely low to get low ripple; it only has to be several times less than the reactance for the capacitance to dominate the ripple voltage, which it will be in a non-defective capacitor.

The value of capacitance is what is chosen to give the desired ripple voltage without regard to ESR. ESR need not be considered when choosing a cap for desired ripple because for a good cap, ESR has little effect on ripple. ESR has an effect on internal heating of the capacitor, and should be taken into account for that reason, but it need not be considered with respect to ripple voltage for non-defective capacitors (having low DF, in other words), regardless of load.



Why would one suppose that the cause of increased ripple is increased ESR, rather than decreased capacitance?



Ripple voltage does indeed depend on the load, even if ESR is zero.

But dependence of ripple on load isn't the major reason why we can't be sure if the ESR has increased or not.

I agree that ESR can increase quite a bit (if the capacitor is not defective to start with) before we see more ripple. The reason for this is because a properly designed filter would use non-defective capacitors to start with. For such caps, the DF is low, meaning the ESR is substantially lower than the capacitive reactance, and the ripple is not much determined by the ESR, regardless of load. If the capacitor is becoming defective, since the ESR to start with when the cap was new was much less than the capacitive reactance, it can increase quite a bit before its effect on ripple is noticeable; the ratio of ESR to reactance is telling the story here.



I'm saying that what DF (the ratio of ESR to reactance) can tell us is whether increasing capacitance while keeping ESR constant is going to reduce ripple voltage. Your examples above are of a different scenario and they don't show that DF doesn't indicate what I describe in post #144..



Again, the reason for considering the ratio of ESR to reactance is with respect to the question of whether increasing capacitance with a fixed ESR will reduce ripple voltage. With respect to this question, load doesn't come into it at all. There are other things to consider, but this is the only view I was considering, and with respect to it, the ratio of ESR to reactance is the relevant factor.

Hello again,


[1]You said:
"Note that when the cap is increased to 20000 uF with an ESR of .15 ohms, the DF becomes 2.26; this is what we would have if the capacitor were defective, so we shouldn't be surprised that if such a bad capacitor were used, the ripple voltage would be high. When I used to repair electronics, seeing a high ripple on a supply line was the first sign that the filter cap was bad."

[2]Then later you said:
"Ripple voltage does indeed depend on the load, even if ESR is zero."

[3]And also you said:
"Why would one suppose that the cause of increased ripple is increased ESR, rather than decreased capacitance?"

If you believed in #2, then why would you assume that the cap was bad in #1 ?
This leads me to believe that you were saying that the ripple voltage is determined mostly by the cap and ESR and has nothing to do with the load, but then later modified that stance.
#3 just seems to add to the confusion...why would one suppose the ESR went up *OR* the capacitance went down, when the load could have increased? If you believed that the ESR and capacitance where the only players in the ripple voltage then this is exactly what you would conclude: that the cap was bad.

In short however, what i am saying for the most part is that in a circuit with four components in it, it is not a good idea to look at only two of them in order to determine anything about some single node, unless you have previously set boundaries on what works and what doesnt.
I had no problem agreeing that the ESR and Cap value had a relationship of their own with respect to an increase of one or the other, that was never an issue, and i even stated that myself when i showed the data for various caps and ESR values. But i did argue that the ripple depends on the load too, not just the ratio of ESR to cap value, and by your previous statements you did not seem to agree with that and that is why i talked about it. If you agree now but not before that's fine, or if you agreed all along that's fine too but your statements did not seem to imply that at all as you can see from the above quotes, so i replied with respect to that implication.

On a more positive and less confusion note (he he) i am closer to an analytical solution for the circuit with series resistor and capacitor ESR and even non ideal diode, but i am not sure if i will pursue this to completion or not yet.
I have worked out an analytical/sequential solution however which probably gives accuracy down to the nano volt with 16 digit floating point, and better with a better computing machine as there is no limit with this kind of solution either.

One of the interesting things about this is how complicated a simple circuit can be mathematically, even though it only contains a few components and we've all used it many times in the past without giving it much thought.

 

[MrAl]

Hello again,

I decided to tackle the circuit with series resistance Rs, capacitor ESR as Rc, and of course the capacitor C and load resistance R, and full wave bridge rectifier.

The difficulty arises because the cap ESR (Rc in the equations) makes the equations much more complicated. However, there is a general solution that is amazingly simple. Well, at least the solution equation in it's most general form is simple, but what i find interesting is that it can be written so simply, almost like a law of nature. Maybe call this the "Law of Full Wave Rectifiers" <chuckle>, as it may work with any full wave rectifier circuit (Equation 1 anyway). I havent confirmed this yet, but it does in fact represent an exact solution to the full wave rectifier with parts described above: the cap, the load R, the series Rs, and the cap esr Rc.

Equ 1 is the most general equation. It is a partial differential equation because there are three to four variables. I found a solution to this equation but it's not that simple, so there may be more simple solutions. Equ 1 breaks up into Equ 2 for this circuit. Everything in Equ 2 is a variable, so the solution isnt very simple. Everything depends on everything else, which makes it seem impossible to solve, but it is in fact solvable. Equ 3 shows how vc0 (also a variable) is calculated (but only for this particular circuit) and this is where the familiar factor "K" comes into play (K=0.9 for 90 percent ripple as measured from the peak of the output voltage). Equ 4 is just there to check the other solutions and modify C if needed. There is a chance that Equ 4, the obvious exponential, isnt needed, even though it appears that the solution depends on the falling exponential we are all used to seeing now that occurs between peaks. Amazingly, the solution may be possible without considering that exponential, but i havent verified this yet. I do know that i got pretty close to the right cap value without considering the exponential.
What else is interesting is that the output peak is fairly constant, regardless of capacitor value C.

I would like to publish the entire solution but i am trying to figure out where the best place to put it would be. Maybe an article?

Equations are found in the attachment.
I almost forgot to mention that "td" is the time where the diode switches to 'on', and is a variable because it also has to be determined by solving the equation(s), but those equations are sufficient to calculate everything, and as mentioned, there is a chance that the last equation is not needed, except as a self check.

 

[analog1]

energy stored in a capacitor =1/2 CE square joules [watts -second]
energy stored in an inductor = 1/2 LI square [watts-second]
ε =2.718 L = henries Cin farads E in volts I in amperes
have fun

 

[MrAl]

energy stored in a capacitor =1/2 CE square joules [watts -second]
energy stored in an inductor = 1/2 LI square [watts-second]
ε =2.718 L = henries Cin farads E in volts I in amperes
have fun

Hello there,

If you are suggesting that there might exist an energy balance equation that can be solved in order to eventually solve for the capacitor value, you are probably right. But i did not pursue that path mainly because i wanted to follow what we were doing with the simpler circuits before this one came up, and also just to see if it was possible to formulate in a simple way from that perspective.

To form a solution based on an exact energy balance, we'd have to be able to write equations for the energy in all of the components for all time. If you want to pursue this then please show your results here, or at least your attempts.

Before i forget to mention, these circuits with input inductors are often easier to analyze because they can be calculated base on the "energy" in the inductor. There is a balance concerning the volt seconds of the inductor.

 

[Hubert]

**broken link removed**

I think something is going wrong while trying to follow that link.

 

[Ian Rogers]

I think something is going wrong while trying to follow that link.

As a new member you would probably not realize the ETO had a major hard drive issue some years back... Loads of images were destroyed...

 

[Hubert]

Hello again,

I find that the diode and extra series resistance dont change the ripple percent as much as it changes the output peak and average DC output. They subtract from the input voltage so that's no surprise.

Shown in the attachment is the calculation for a full wave bridge setup with spice diodes and series resistance using a semi analytical approach which is much faster than a simulation. The calculations are embodied in the program and that calculates the percent ripple as well as peak and dip.

This is for full wave, and you can see by the results that the diode and input resistance help to filter a little as we only needed a 65uf cap to get 10 percent ripple. Note however that the peak is much lower than it would be with an ideal diode.

Hello MrAl

If it's possible where I can take a real look on your calculator?
Thanks in advance.
Hubert

 

[Hubert]

As a new member you would probably not realize the ETO had a major hard drive issue some years back... Loads of images were destroyed...

Oh that's really a pitty. May be I'm wrong - but I'm thinking to have a small chance because the requested part was published by the middle of the year and not years ago?

 

[MrAl]

Hello MrAl

If it's possible where I can take a real look on your calculator?
Thanks in advance.
Hubert

Hi,

You mean you would like to try out the calculator shown in the image?
I suppose i can upload the program if you'd like to try it, maybe it would upload as a zip file.

 

[Hubert]

Hi,

You mean you would like to try out the calculator shown in the image?
I suppose i can upload the program if you'd like to try it, maybe it would upload as a zip file.

Hello Al.
Sure. It takes me now 2 days following the discussion getting an overwiew. I'm not at the end now. I'm intending to get closer with that stuff. It would be nice if you do so.
Hubert

 

[MrAl]

Here it is, see if you like it. Tested under Win7 mostly.
You probably want to save the file before running it.
Calculation time may vary.
NOTE: See updated version 2.00 later in this thread which includes the cap ESR.