I have a regenerative receiver working and receiving stations. It amplifies RF through a 2N3904 transistor. There is a potentiometer (500 ohm) on the emitter of the 2N3904 and a fixed resistor of 1.8 K ohm in series leading back to negative potential. When this potentiometer is closed (not sure is that is the term but it now provides no resistance to the AC signal), then the receiver will begin to oscillate. A buzz is then heard in the earpiece. If this potentiometer is then turned so its resistance increases a little, the buzz stops in the earpiece and any station tuned with the variable capacitors on the turning circuit will be audible.
I copied the circuit for this receiver from a website and have little idea of how it was designed. I can see it has a figure of eight network of resistors which voltage-divide the bias into the base. I think I just got lucky that this combination of resistor values delivered a Q-point that was in the right place on the load line.
Or did I get lucky?
I would appreciate any comments you might make about my circuit - does it deliver to the correct place on the load line or do I need to work some more?
I am also curious about how the fixed capacitor values around the transistor can be calculated.
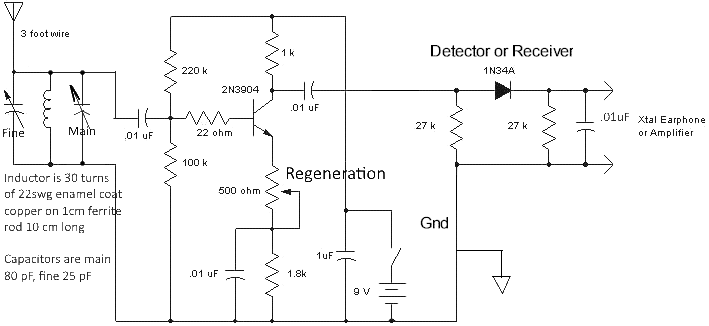
I copied the circuit for this receiver from a website and have little idea of how it was designed. I can see it has a figure of eight network of resistors which voltage-divide the bias into the base. I think I just got lucky that this combination of resistor values delivered a Q-point that was in the right place on the load line.
Or did I get lucky?
I would appreciate any comments you might make about my circuit - does it deliver to the correct place on the load line or do I need to work some more?
I am also curious about how the fixed capacitor values around the transistor can be calculated.

