SOME INSIGHT INTO THE DIVERGENCE
See the attachment while reading this post.
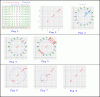
Fig 1:
The flow field equation F, the div calculated, the flow field drawn with small arrows
where the small red points are the tips of the arrows representing the vectors.
Note the vectors are drawn as 1/2 of their actual length to make the drawing more clear.
Fig 2:
The field drawn a little better but only along the diagonal in the first quadrant.
Vector lengths drawn here reflect their actual length.
Fig 3:
A circle of radius r drawn with the same scale not showing the field, but instead
showing the outward unit normals from the circle (green). The outward normals have direction.
Fig 4:
The circle and outward normals with the field (along the diagonal) drawn. It is
observed that the field does not always point in the same direction as the
outward normals. Some point in the same direction (upper right) and some point
opposite to it (lower left).
Fig 5:
Since Fig 4 doesnt show all the field vectors, it should be clear that the vectors
cross the border of the circle all around the circle not just along the diagonal.
Thus, they cross sometimes in the same direction, sometimes opposite, and
sometimes perpendicular, and sometimes at various other angles to the normals.
Fig 6:
Same diagram with the outward normals removed for clarity. The lengths of two
of the vectors along the diagonal are marked L1 and L2, with L2 being the longer
one. L2 is always the one leaving, L1 always the one entering.
Fig 7:
Same diagram except now we see the circle drawn smaller. The circle is smaller so
the area is less than in figure 6. Note also that the vector leaving the circle
now is smaller than the one leaving in figure 6. So the difference in length of
L2 and L1 has gotten smaller as well as the area of the circle.
Fig 8.
The circle is even smaller now, and thus would have a smaller vector coming out of
it's upper right side, so the difference in length between the large vector
(had it been drawn here) and the small vector will be even less than before, and
also the area of the circle has surely decreased.
Now for the math that ties all these together...
The flux f1 from the small vector with length L1 is simply the length of the vector.
However, since there are many vectors entering the circle on that side we need a way
to account for all of those vectors without having to calculate each and every one
(which we could do if we wanted to take that much time and rigor). So to make it
a bit simpler to calculate, we note that if all of the vectors were at the same angle
they would all enter at the same angle, and the ones leaving would also leave at the
same angle. But also, some of the ones entering will not be in line with the normals
but then an equal number leaving would also not be in line but would be at the same
angle except their direction is outward instead of inward. So to keep this simple
we make the flux entering the circle equal to half the circumference of the circle
(half because that's the only border that is crossed by those influxes) times the
length of that one flux vector:
Fin=2*r*pi/2*L1=r*pi*L1
and following the same logic we do the same for the outgoing vectors:
Fout=r*pi*L2
except of course that we multiply by that one outgoing vector L2.
Ok, so the flux in is Fin and the flux out is Fout, so the total flux
leaving the circle is:
Ftotal=Fout-Fin
Now the area of the circle is:
A=pi*r^2
and the Div is the net total flux divided by the area (in 3 dimensions it would be the flux/volume):
Div=Ftotal/A
So to calculate the Div we calculate the lengths of the two vectors L2 and L1 from
the flow field equation:
F = 0.2*x i + 0.2*y j
at the two points x1,y1, and x2,y2, multiply by half the circumference, take the difference,
then calculate the total area of the circle, then divide.
So lets start with the bigger circle.
For the big circle we have points:
x1=1, y1=1, and
x2=3, y2=3
Now we do point 1 first:
Fx(x1,y1)=0.2
Fy(x1,y1)=0.2
and L1 is just the norm:
L1=sqrt(0.2^2+0.2^2)=0.2828 approximately
And now for point 2:
Fx(x2,y2)=0.6
Fy(x2,y2)=0.6
and L2 is just the norm:
L2=sqrt(0.6^2+0.6^2)=0.8485 approximately
The circle diameter is:
dia=sqrt((y2-y1)^2+(x2-x1)^2)=2.828 approximately
and so half the circumference is:
C2=dia*pi/2=4.442 approximately
so the estimated total flux entering is:
Fin=L1*C2=1.256
so the estimated total flux leaving is:
Fout=L2*C2=3.769
Note we have quite a bit more leaving than entering.
The total flux across the border of the circle is:
Ftotal=Fout-Fin=3.769-1.256=2.513
The circle radius is half the diameter:
r=dia/2=1.414
so the area is:
A=6.281 approximately
so the Div is:
Div=Ftotal/A=2.513/6.281=0.4000955 approximately.
The Div calculated from the standard way to calculate it is 0.4 so this is our first approximation.
We did get a little lucky here though in that our first approximation came out so close. This
most likely will not happen with more complex fields so we'd have to decrease the circle size
and look at the smaller vectors to get a better approximation.
Also keep in mind that we really should have calculated more crossing vectors and summed
the results. Maybe next time

[LATER]
The numbers look accurate (at least accurate enough) so i guess there is nothing more to do. We could let the circle becomes smaller and smaller, but since we've already got the right number it seems a waste of time to do that with this example. What should happen with most fields is as the circle gets smaller and smaller we should see the Div calculated this 'long' way match closer and closer to the Div calculated in the normal way.
Just one small note about the sign of Div...
When the Div is calculated the sum of vectors leaving the circle was larger than those entering the circle, so the result was positive. If the sum of vectors leaving is smaller than the sum entering then the result will be negative (L2 is the length of the vector leaving and L1 is the length of the vector entering, and since L2>L1 then L2-L1 is positive, but if the vector leaving (L2) is smaller than the one entering (L1), then of course L2-L1 will have to be negative).
In three dimensions we could not use a circle but instead would have to use a sphere. While the circle can 'sense' direction in any plane angle, the sphere unit normals are omnidirectional in all three dimensions so it can 'sense' direction from any solid angle. Here we would have the 3d vectors crossing the surface of the sphere instead of the border of a circle, and the inside of the sphere is a 3d volume not an area. To get the Div we could use smaller and smaller spheres and as the spheres get smaller and smaller the approximation would get closer and closer to the actual Div in three dimensions.
Just one additional small note about the drawing of the circles as they get smaller and smaller...
The circles drawn in the diagram near the bottom get smaller and as they do it is clear to see that the vectors crossing the border of the circles get smaller as the circle gets smaller, but in those drawings we allowed the center of the circle to move along the diagonal when really we would not do that. We would instead keep the smaller circles centered around the same x,y point as the larger circle so only the diameter would change, not the location. The circles drawn however do show the same thing as far as the vector lengths are concerned, in that they do get shorter as the circle gets smaller. Drawing the circles all centered at the same point allows us to state that the divergence at that one point is what we calculated. For this field the Div is the same at any point, but for other vector fields this very well may not be the case so it is better to think of the circles as being all drawn at the same center point no matter what their radius is. I could update the drawing but it would be harder to see the vectors getting smaller, and it's not too hard to imagine the circle getting smaller but staying centered at the same point as the larger circle.