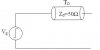
In our class, we described the voltage and the current across/in a transmission line as the sum/difference of progressing wave and regressing wave:
I(z,t) = I+(z,t) - I-(z,t)
V(z,t) = V+(z,t) + V-(z,t)
And that:
I+(z,t) = V+(z,t) / Zo
I-(z,t) = V-(z,t) / Zo
(Zo is the characteristic impedance of the transmission line).
In the bellow picture, I calculated I(z,t) and V(z,t) for t->∞.
V(z,t->∞) turned out to be equal V-(z,t->∞) = Vg (a regressing wave) which makes sense since in the steady state (t->∞), there is no voltage drop across the line.
But it turns out that (according to the above formulas):
I(z,t->∞) = -Vg /Zo.
How come there's current through the line, in steady state (t->∞) ?
Thanks.
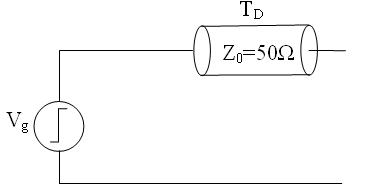
I(z,t) = I+(z,t) - I-(z,t)
V(z,t) = V+(z,t) + V-(z,t)
And that:
I+(z,t) = V+(z,t) / Zo
I-(z,t) = V-(z,t) / Zo
(Zo is the characteristic impedance of the transmission line).
In the bellow picture, I calculated I(z,t) and V(z,t) for t->∞.
V(z,t->∞) turned out to be equal V-(z,t->∞) = Vg (a regressing wave) which makes sense since in the steady state (t->∞), there is no voltage drop across the line.
But it turns out that (according to the above formulas):
I(z,t->∞) = -Vg /Zo.
How come there's current through the line, in steady state (t->∞) ?
Thanks.
Attachments
Last edited: