Imagine a semi-infinite flat copper surface; for example, if half the universe were filled with copper and presenting a flat surface to the half that wasn't full of copper. When an electromagnetic wave would impinge on that flat surface, the current density in the copper would decrease with distance penetrated into the copper. The mathematical function describing the decay of the current density would be the exponential function. At some depth below the surface, the current density would have decayed to a value 1/e = .368 times the current density at the surface; this is called the skin depth. As you go deeper into the copper, the current density continues to decrease until it vanishes into the atomic noise level, because there is an infinite depth of copper for it to penetrate.
If the copper isn't infinitely deep, for example, a sheet of copper .001" thick, at low frequencies (high audio perhaps) the current density hasn't attenuated to near zero by the time we get to the other side of the copper sheet. A thin copper sheet can't provide much shielding against low frequencies.
The situation with a copper wire is not like the infinitely thick copper half universe, or a finite but very thick copper sheet.
At frequencies where there is noticeable attenuation (but not too much) of the surface current density, what happens is that the current density decreases as we move from the surface of the wire toward the center, and if we continue to proceed past the center and back toward the surface on the other side from our starting point, the current density begins to increase again until we reach the surface. The current density at the center of the wire doesn't reach the atomic noise level.
If the frequency is low enough (but we still see some attenuation), the current density at the center of the wire will not ever decrease to as little as 1/e=.368 times the surface value of the current density. In this case, what is the skin depth? When we were considering the very deep half universe of copper, the current density
always reached 1/e times the surface density.
So it happens that the very concept of skin depth is defined in terms of an AC current decaying in a thick piece of copper with a large plane surface of very large extent (infinite in the ideal case). This is not the situation where a wire with circular cross section is concerned. The surface of the wire which the AC current is penetrating is not flat--not a plane. This leads to behavior which is very different from the case of penetration into a plane surface
when the skin depth is not much different from the wire radius. In that case, the rate of decay of the current density is not well approximated by an exponential function; it happens that Bessel functions must be used.
But when the skin depth is very small compared to the wire radius, then the exponential approximation is good. See this explanation from Ramo, et al:
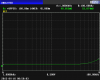
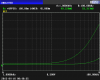
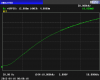
Figure 5.16 (b) shows the case where the exponential approximation fails. The solid line shows the actual current density with depth, and the dashed line shows the exponential approximation. When the attenuation is not very great, the difference in the two curves is fairly great. When the attenuation is great, the difference in the two curves is not very large.
What all this means, is that calculating Rac/Rdc when the skin depth is nearly the same as the wire radius by means of an exponential decay in the current density will have a large error. If the skin depth is small with respect to the radius, then the exponential functionality will give reasonably accurate results.
As it happens, finding analytical expressions for various geometries of conductors is extremely difficult, but besides the case of a flat plane surface the other simple geometry where an exact analytical expression is known, is the case of a wire of circular cross section. Ramo, et al. give the result, which involves Bessel functions:
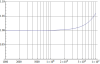
The tables in the old NBS circular No. 74 were produced like this using Bessel functions; here's a plot rather than tables. This is the same graph found in Terman's "Radio Engineer's Handbook":
For cases where the analytical solution hasn't been found, numerical FEA analysis comes to the rescue. This is especially useful for transformers and inductors where proximity effect is dominant.