Totally unsuitable wire used for SMPS transformer (skin effect)?

[Flyback]

Hello,
Do you believe that the 60W flyback SMPS transformer on page 21 of AN3089 (see below) has been wound with massively over-expensive multi strand wire?
The primary has been wound with turns of 30 x 0.1mm wire, and the secondary with 90 x 0.1mm turns.
This is far too expensive, and pointless, because the skin depth of copper at 85KHz is 223um.
So why have they used such totally unsuitable, overly expensive wire?
Also its worth remembering that this is a quasi resonant flyback, and the primary and secondary currents are trains of triangles, which have an overall DC level. Obviously the DC level is not in any way impeded by the skin effect.
AN3089:
https://www.st.com/st-web-ui/static...tion_note/CD00252755.pdf?s_searchtype=keyword

 

[ronsimpson]

switching frequency at about 165 kHz

from the .PDF page-5 and page-12

Mr. Flyback, You use adjective with ease.

massively over-expensive

far too expensive

such totally unsuitable

overly expensive

Obviously

 

[crutschow]

That multi-stranded Litz wire is a common way to reduce wire resistance in high frequency transformers due to the skin effect.
It is not at all pointless to use in this application.
Since the skin depth is so thin at those high frequencies (as you calculated), many strands of fine wire are used to get more surface area for a given amount of copper, and this gives less resistance (the ideal would be hollow wire and thus large copper pipes are sometimes used for carrying high power RF signals).
And whatever the waveform is in the transformer, it has may high AC frequency components that generate a skin effect.

 

[MrAl]

Hello there,

A formula i had developed a while back for the skin depth:
d=1361/(6641*pi*sqrt(f))

where f is the frequency in Hertz and d is the depth in meters.

Now if you use that formula to calculate the required radius of a wire to be used at 100kHz (radius is half the diameter) you would come up with 2e-4 or 0.2mm which is the radius of a AWG #26 gauge wire.
However, this is the maximum size wire recommended by companies like the old Magnetics Inc. Why is that the maximum size and not the best size?

The answer is because there is still quite a bit of loss using #26 gauge wire even though the skin depth is equal to the radius, and that is because the skin depth is not a magic number where we get perfect, normal conduction before that depth and then none, as that view is the simplistic view which is usually used just to begin to understand skin depth and not intended to be used to understand the full breath of the problem.

Looking at skin depth a little closer, we find that near the surface we get normal conduction, but as we get deeper into the wire the conduction becomes less and less, even though we have not yet reached the skin depth. So as we go deeper we get less and less conduction and that means that we always loose some conduction, no matter what wire size we use. We use that outer shell view to simplify the problem but really we need to know the ratio of the AC resistance to the DC resistance at a given frequency, and we can find this by knowing the skin depth or we can just use a formula for that. But in any case, using a wire that has the same radius as the skin depth means there will still be losses in the wire due to the AC current, and in #26 wire at 100kHz the extra loss could be as high as 35 percent, which could be significant if we want a high efficiency converter.

So how about using a slightly thicker gauge wire? That will help for sure, because the outer shell of conduction becomes larger, but we do use more copper that way and that means it takes up more room on the core bobbin. So how about using two wires of gauge 3 times larger than that? That will help also, because then the ratio of copper used to copper wasted goes up, and since the skin depth is the same as before there will be less AC resistance.

To see how multiple strands can help we just need to look at the 'resistor' (the wire) as a three dimensional problem instead of the usual symmetric two dimensional problem. We loose the symmetry going from surface to axial because the resistance is no longer constant along any radial line but actually becomes exponentially decreasing. If we use a thinner wire, then we have less depth which means the resistance decreases less. To get the full conduction we need however, we have to add more strands that are not electrically in contact with each other, and wound in such a way that other effects dont bother the conduction either. Wire makers know about this and so they weave the wire in a certain fashion.

So if you see multiple strand wire being used it might be because they are going for the highest efficiency possible. If you use something other than that you risk loosing efficiency, although the efficiency you loose will depend on the operating frequency and the wire size you choose. Note also that if you have a lot of room left on the bobbin (or just the window area) then you can use heavier gauge wire with the side effect of the construction just being heavier. If you dont have room on the bobbin though then you are stuck with using multi strand wire.

A quick functional explanation would be to look at a the total resistance for a normal resistor with a DC current:
R=4*rho*L/(D^2*pi)

and we can see dimensions length L and diameter D and rho is the resistivity of the material.

To account for skin depth, we have to take into consideration the change in resistivity with frequency and depth, which means rho becomes a function of those two, so the formula becomes:
R=4*rho(f,r)*L/(D^2*pi)

where we can see that rho is now a function of frequency 'f' and depth along any radii 'r'. The function is a decreasing exponential so we see the change in resistivity decrease as we go deeper (r becomes larger).
The main point being that it is not a quick drop off but a gradual change that starts at the surface and ends at the axial center of the wire.


Examples:

AWG #26 has resistance 1.35 times its DC resistance at 100kHz.
AWG #22 has resistance 1.59 times its DC resistance at 100kHz, but comes out lower than #26 anyway.

AWG #26 1000 feet long has AC resistance 55 ohms at 100kHz.
AWG #22 1000 feet long has AC resistance 26 ohms at 100kHz.

As a final note, recall that a square wave has harmonics that have amplitude 1/n of the fundamental, so the third harmonic amplitude is 1/3 of the operating frequency, and we dont want this to be too attenuated either so at 100kHz that means we are now dealing with 300kHz instead, although at reduced amplitude.
If the wave is a triangle then we have harmonics of about 1/n^2, so that means the third harmonic (again at 300kHz) accounts for 1/9 th of the signal level, which still may be significant in a very high efficiency converter.

 

[The Electrician]

To account for skin depth, we have to take into consideration the change in resistivity with frequency and depth, which means rho becomes a function of those two, so the formula becomes:
R=4*rho(f,r)*L/(D^2*pi)

where we can see that rho is now a function of frequency 'f' and depth along any radii 'r'. The function is a decreasing exponential so we see the change in resistivity decrease as we go deeper (r becomes larger).

The resistivity of copper in a wire does not change with depth.

 

[KeepItSimpleStupid]

FB:

Your also off by a factor of 10. 85 kHz is 0.00085 MHz; 0.00085 MHz * 1000 kHz/MHz = 85 kHz

https://chemandy.com/calculators/skin-effect-calculator.htm

 

[MrAl]

The resistivity of copper in a wire does not change with depth.

There is in fact a change in conduction with depth (and frequency) and that can be viewed as a change in resistivity. If you are uncomfortable with this you can change that formula to contain a function of conductivity instead of resistivity but it will only come up with the same result, assuming the first result was correct to begin with of course.
More traditional methods use a decrease in area as the quantity that changes, which also results in less conduction. The actual copper wire area never changes, yet they use a decrease in area to account for the effect within the formula and might call it the 'effective' area. So if you like we can call the former the 'effective' resistivity.

 

[MrAl]

FB:

Your also off by a factor of 10. 85 kHz is 0.00085 MHz; 0.00085 MHz * 1000 kHz/MHz = 85 kHz

https://chemandy.com/calculators/skin-effect-calculator.htm

Hello,

I will double check the numbers later today.
0.00085 MHz is 850Hz.
Also, i do get the same skin depth as on that web site at 100kHz for copper. They use 0.999991 for the relative permeability and i used exactly 1.
Their skin depth at 100kHz comes out to 206.1665um and mine comes out to 206.2884um, so the difference is about 0.05 percent which i dont view as significant for an estimate like this where there are other factors which will throw off the answer slightly anyway.

Also, the skin depth itself doesnt mean that much because it doesnt help much to know the skin depth unless you are familiar with a few different wire gauges and their overall effect on some design already. The better quantity to know is the ratio of AC resistance to DC resistance, or just the outright AC resistance. That really tells you what you have right there at hand. If the AC resistance is 55 ohms you'll know whether that is too high for the design, but if you look at the skin depth you wont know for sure unless you happen to know what skin depths are acceptable already which is a little too comparative for my taste. I would rather know the actual AC resistance or at least the ratio of AC to DC resistance.

So check out the calculator for AC resistance they have, and see if you can find the fault with it. Hint: note how their #26 wire 100kHz AC resistance comes out so close to the DC resistance for say 1000 feet.
As they say, dont trust anything on the web without a second source

 

[schmitt trigger]

My experience with demo boards and/or app notes is that a vendor will optimize the design shown for a parameter or group of parameters.
From a quick look at the app note, it seems that ST Micro is mostly concerned about efficiency.

But as an user, one should take a good look at the reference design, and decide which parameters are important. It may be that one can sacrifice a little efficiency in order to reduce cost. It may be that one has different component vendors which one would prefer. There are myriad possibilities, and there are tradeoffs between all of them.
Remember, engineering is the art and science of tradeoffs.

 

[Flyback]

thanks, in addition, I don't understand the concept of R(ac)/R(dc) = 1, because for any given wire, R(ac) is always greater than R(dc), surely?

 

[MrAl]

thanks, in addition, I don't understand the concept of R(ac)/R(dc) = 1, because for any given wire, R(ac) is always greater than R(dc), surely?

Hi,

I dont know anyone who would say Rac/Rdc=1 without giving more information such as that the frequency is also very very low. The ones that use a 'single shell' physical model will try to say this for a wire who's skin depth at a given frequency forms a conducting shell with radius equal to the skin depth and who's conductance is the same as copper for any depth within that shell depth, but that cant be right because at the skin depth the conduction is reduced to almost one third. So for example say we have a DC resistance of 40 ohms, and the if the whole shell had the same conduction as copper then the AC resistance would be 40 ohms too, but if the whole shell had one third the conduction then the resistance would be 120 ohms. So we must have a true AC resistance more than 40 ohms but less than 120 ohms, but it cant be real close to 40 nor real close to 120, and as it turns out it comes out closer to 55 ohms at 100kHz. Closer to 40 ohms but still significantly different than 40 ohms.
The right way to do it is to use the method of cylindrical shells, where each discrete shell has less and less conduction, and then let the thickness of each shell wall approach zero and sum over the radius. A little tricky but not too bad. At the very least, choose 10 discrete shells and calculate the total based on those 10 shells where each one has a different conduction.

But the simpler view is just that the AC resistance is always higher than the DC resistance:
Rac>Rdc

except for very very low frequencies where it just doesnt matter anymore. Maybe 1Hz

The rule for wire thickness is to go down in wire gauge by 3 units to get twice the conduction (half the resistance), so if we go up 3 wire gauges we get double the DC resistance, but when we put two in parallel we get back to the original DC resistance but we end up lowing the AC resistance because the smaller wire gauge handles the AC current better. Sometimes it's not by much however, but it may make a difference when you're after the maximum efficiency.

For example, at 100kHz we have about 55 ohms at 100kHz with AWG 26,
and if we go up in wire size to AWG 29 we have about 101 ohms at 100kHz, but if we use two wires arranged properly we can get down to about 50 ohms which is a little less.
If we go up three more sizes to AWG 32, we have about 192 ohms, and four of these in parallel would ideally give us about 48 ohms.
At 500kHz the difference will be more however with those same gauge wires:
AWG 26: 75 ohms
AWG 29: 129/2=64 ohms
AWG 32: 229/4=57 ohms
approximately.
At 300kHz is not as good as 500kHz but better than 100kHz, but had this been a 100kHz square wave then we would want to think about all three of these frequencies and the effect it has on the different harmonics. If we loose too much of a significant harmonic then the efficiency has to go down, even though it might lead to better EMI stats.

 

[The Electrician]

There is in fact a change in conduction with depth (and frequency) and that can be viewed as a change in resistivity. If you are uncomfortable with this you can change that formula to contain a function of conductivity instead of resistivity but it will only come up with the same result, assuming the first result was correct to begin with of course.
More traditional methods use a decrease in area as the quantity that changes, which also results in less conduction. The actual copper wire area never changes, yet they use a decrease in area to account for the effect within the formula and might call it the 'effective' area. So if you like we can call the former the 'effective' resistivity.

What I'm uncomfortable with is that resistivity is a well defined property of matter: https://en.wikipedia.org/wiki/Electrical_resistivity_and_conductivity

and you are misusing it.

Resistivity does not change with depth, and neither does conductivity, assuming conductivity is defined as the reciprocal of resistivity.

 

[MrAl]

What I'm uncomfortable with is that resistivity is a well defined property of matter: https://en.wikipedia.org/wiki/Electrical_resistivity_and_conductivity

and you are misusing it.

Resistivity does not change with depth, and neither does conductivity, assuming conductivity is defined as the reciprocal of resistivity.

Hi there,

Well, the point i was making was, so is cross sectional area, The area is a well defined measurement yet traditionally no one has a problem with redefining the area to account for a change in properties even though it will not be the actual measured area anymore.

We can call it the AC resistivity then, if you feel more comfortable with that. Otherwise i'd have to change the formula to show the apparent (not real) change in area which would make it look like we were squeezing the wire from all radial directions
In any case though, the final result would come out the same.

I found it more comfortable to deal with the change in conductance or resistance as the depth increases, and many other web sites quote the same.
To paraphrase a few:

"The skin effect causes the effective resistance of the conductor to increase at higher frequencies where the skin depth is smaller, thus reducing the effective cross-section of the conductor."

"Frequency dependence of resistance:
Another complication of AC circuits is that the resistance and conductance can be frequency-dependent. One reason, mentioned above is the skin effect."

The alternative is to either change the effective cross sectional area or rework the formula into one which uses the current density to account for the change in resistance. But is this really necessary?

Also note that we cant call it impedance or anything like that because it is really the "AC Resistance" that we are after, so to me it makes sense to call the resistivity due to an AC current (rather than to a DC current) the "AC Resistivity".

 

[KeepItSimpleStupid]

A page I visited, called it the derating factor which is a typical term. The online calculators happen to use resistivity as an input.

 

[The Electrician]

I found it more comfortable to deal with the change in conductance or resistance as the depth increases, and many other web sites quote the same.
To paraphrase a few:
"The skin effect causes the effective resistance of the conductor to increase at higher frequencies where the skin depth is smaller, thus reducing the effective cross-section of the conductor."

"Frequency dependence of resistance:
Another complication of AC circuits is that the resistance and conductance can be frequency-dependent. One reason, mentioned above is the skin effect."

Resistance and conductance are not the same thing as resistivity and conductivity. Resistivity and conductivity are intrinsic properties of the copper. Resistance and conductance (of a piece of wire, for example) are the result of taking into account the geometry of a piece of copper and where the connections to it are made.

The resistance of a piece of wire at DC is given by R = rho*L/A, where rho is the resistivity, L is the length of the piece of wire, and A is the cross sectional area of the wire. At AC the resistance is different due to skin effect causing the current density to vary across the cross section of the wire, not rho. rho is the same everywhere in the copper at DC and AC frequencies below gigahertz frequencies, which is the region we're discussing.

In an earlier post you said:

Hi,

If we look at the effect along the radius of a long wire the current density changes as an exponential. Integrating over the radius using this exponential as a weighing function provides us with the following formula:
r=2(g^2*(e^(-1/g)-1)+g)

where
g=1361/(6641*pi*sqrt(f)*R)

for copper wire, and
f is the frequency in Hertz and R is the radius of the conductor in meters,
and r is the ratio of DC resistance to AC resistance, so an r value of 0.5 for example means the AC resistance is 2 times higher than the DC resistance.

This formula is not like the formula where we assume that the penetration depth is only equal to the skin depth, and obtain the AC resistance from that. That formula is limited because the approximation falls short when the radius of the wire gets closer to the skin depth. For example, the approximation would give an estimate of close to 0.5555 for a wire with radius three times the skin depth, while the better approximation from the formula above yields an estimate closer to 0.4555.

The skin depth at 100kHz is 0.206mm, which is about equal to the radius of a #26 gauge wire, and using the older approximation this tells us that the AC resistance is about equal to the DC resistance. This is the largest wire size recommended by Magnetics Inc for use at 100kHz. They obviously used the single skin depth approximation to determine this, which isnt too bad really.

However, using the formula above, the DC to AC resistance ratio for an AWG #26 wire at 100kHz comes out close to 0.74, meaning the AC resistance is about 35 percent greater than the DC resistance. This tells us that #26 isnt that bad, but we can of course do better with a larger wire size.

You were using current density as the variable in your calculations; using current density is the thing to do. Current density does vary with depth in the wire, but resistivity does not.

However, your analysis of the case where the skin depth is close to the wire radius is flawed. You say that "If we look at the effect along the radius of a long wire the current density changes as an exponential." This is not close to the truth when the skin depth is near the radius. The exact expression for the current density variation with depth in a round cylindrical wire involves Bessel functions, and is not well approximated by using an exponential when skin depth is nearly the same as the radius.

When the skin depth is very small compared to the radius, then using the exponential is a good approximation. This is discussed in Ramo, Whinnery and Van Duzer. An exact solution to the problem in Bessel functions exists. Also, Terman has a graph showing Rac/Rdc for various ratios of skin depth to radius.

If we take the radius of a 26 ga wire as .202 mm, the exact value of Rac/Rdc at 100 kHz is 1.0179. The expression g=1361/(6641*pi*sqrt(f)*R) gives 1.0212, quite close to the exact value. Your adjustment formula, r=2(g^2*(e^(-1/g)-1)+g), overestimates the value as 1.35

Taking the radius of 22 ga wire as .322 mm, the exact formula gives Rac/Rdc as 1.10745. Your formula gives 1.59.

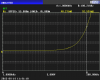
I cut off a 3 foot piece of 22 ga magnet wire and measured the AC resistance versus frequency with an impedance analyzer:

The B marker indicates a resistance at 100 kHz of 52.531 milliohms, and the A marker at 1 kHz shows 48.271 milliohms, for an Rac/Rdc ratio of 1.088, which is fairly close to the exact value of 1.107, and not so close to your formula's value of 1.59

Apparently your technique of viewing resistivity as something that varies with depth doesn't work:

Well, the point i was making was, so is cross sectional area, The area is a well defined measurement yet traditionally no one has a problem with redefining the area to account for a change in properties even though it will not be the actual measured area anymore.

We can call it the AC resistivity then, if you feel more comfortable with that. Otherwise i'd have to change the formula to show the apparent (not real) change in area which would make it look like we were squeezing the wire from all radial directions
In any case though, the final result would come out the same.

 

[MrAl]

Hello again,

What is the make and model of the analyzer you are using to do the measurements?
I am not sure that 3 feet is enough length to test this with, but i will still look over the results and compare anyway. We probably also have to know what the shape of the wire was at the time the measurement was made, and also how it was attached to the measurement instrument.

I cant help if it you dont like the term "AC resistance", "AC conductance", "AC resistivity", or "AC conductivity", but that's how i choose to define it. If the numbers are skewed it is certainly not because of the fact that we 'call' the change in total resistance one thing or another. That one quote i posted previously actually states a change in conductance so that author agrees with my nomenclature convention. So i suggest you drop that silly argument and concentrate on the accuracy issue of the results.

Just to be clear, when the skin depth is small compared to the radius it is the outer shell view that is considered a good approximation. That's the single skin depth used to calculate the 'tube' that is formed as if there was no center to the wire (a pipe not a solid cylinder).
This means that any formula, if correct, must also converge closely to that solution.

 

[MrAl]

A page I visited, called it the derating factor which is a typical term. The online calculators happen to use resistivity as an input.

Hi,

Yes it is always a necessity to input the basic resistivity of the material being used. For copper i think it was 1.7e-8 ohm meters at 20 degrees C but we could look this up.

 

[Tony Stewart]

If you can't figure out how to make a better widget, buy one, until then.

http://www.magnetica.eu/files/News/databrief.pdf

Alot can be learnt from production samples and demos. Then try to break it, testing your theories and fix it. It helps to have a Network Analyzer or a sweep gen sync'd to scope sweep or x out driving the FM gen. to measure stray effects from what you expect. Failing that a step response or better yet, a Bode Plotter. After doing this you calibrate your mind in the geometry measurements of material science , transmission lines , and passive artifacts by coupling in pF and nH or per unit values. Then use your finger, shields, ferrite and other materials to see what Faraday could not, (without an Analyzer) but Maxwell could , with math.

Now they use Spectrum Analyzers to scope xx MVA magnetics before and after shipping many tonnes... to detect any change in geometry of any critical conductors or dielectrics. This gives them a heads up to look for damage risks to fault conditions by the wiggles up to 30MHz in a 50 Hz unit.

In the same respect, winding methods, choice of conductors and stability of the part play a huge role in resonant SMPS performance.

 

[The Electrician]

I cant help if it you dont like the term "AC resistance", "AC conductance", "AC resistivity", or "AC conductivity", but that's how i choose to define it. If the numbers are skewed it is certainly not because of the fact that we 'call' the change in total resistance one thing or another.

You can choose to define any terms that you use however you wish. But when you define them in ways that are not consistent with the way the rest of the scientific/engineering community world wide defines them, your analysis becomes questionable. Why would you want to call the change in total resistance anything other than " change in total resistance"? That's not the problem anyway. The problem is that you said resistivity changes with depth. The word "resistivity" in accepted usage denotes a material property that doesn't vary with depth in the wire. The word "resistance" denotes something else.

That one quote i posted previously actually states a change in conductance so that author agrees with my nomenclature convention.

There's no dispute over whether conductance (of the wire) changes with frequency; it does. But conductivity is a different thing and it doesn't change with depth or frequency.

What is the make and model of the analyzer you are using to do the measurements?
I am not sure that 3 feet is enough length to test this with, but i will still look over the results and compare anyway. We probably also have to know what the shape of the wire was at the time the measurement was made, and also how it was attached to the measurement instrument.

The measurement was made with a Hioki IM3570. The instrument can resolve 1 milliohm and three feet is more than enough. The wire was attached to the standard fixture on the front of the instrument. The fixture terminals are close together, so the wire is in a loop with the largest possible diameter to keep the wire away from itself as much as possible.

Here is the same measurement performed on an Agilent 4294. This measurement gives a value for Rac/Rdc of 54.265 mΩ/48.165 mΩ = 1.127:

And, here is measurement performed on a Wayne-Kerr 6440B, giving Rac/Rdc of 53.69 mΩ/48.47 mΩ = 1.108:

All three results are quite close to the analytical exact result of 1.107, taking the radius of 22 gauge wire as .0322 cm and a frequency of 100 kHz:

Terman's "Radio Engineer's Handbook", on page 30 shows a graph of Rac/Rdc versus an auxiliary parameter: (radius/skin depth). Here is the graph:

Clearly, when the skin depth is nearly the same as the radius, Rac/Rdc is very close to 1.00. Rac/Rdc doesn't approach 1.59 until radius/skin depth is about 4.5

Your formula's result for 22 gauge wire is substantially in error.

 

[Tony Stewart]

As Einstein may have said, it's all Relative.

I prefer to use ESR to cover practically any impedance, if Ohm's Law can be applied in some limited linear way.

So Effectively ESR of a light bulb (oops) rises x10 as it heats up and inrush drops 10:1. It's a resistance but thermally dependant.

Also effectively braided wire & Litz wire has much lower ESR from higher k, fill factor and lower skin effect losses with root(f) and proximity to skin depth but only (Litz) magnet wire has much lower ESL from parallel insulated strands.

Alternate layer wrapping and turn isolation affect interwinding capacitance which affects SRF and together with core choice which affects excitation current, which affects conduction losses and nonlinear saturation losses which significantly reduces L in magnetic cores.

So Effective Impedance and Losses depend on "terms of reference" to: small or large currents, linear or non-linear efftects and harmonic range.

So another way to look at is "effective impedance" from the ratio of utilization of AC/DC currents from geometry of skin effects, but not a change in sacred terms like Resistance or Conductance. ( these are fundamental material properties which are more rigorously defined with physics )

So we may use reference designations like Rac and Rdc but we don't say it is a change in resistance in the proper sense.

(edits)

.