Why is there any voltage even present across the inductor? We always accept a voltage across a resistor without argument because we know Ohm’s law (V = I × R) all too well. But an inductor has (almost) no resistance it is basically just a length of solid conducting copper wire (wound on a certain core). So how does it manage to “hold-off” any voltage across it?
In fact, we are comfortable about the fact that a capacitor can hold voltage across it. But for the inductor, we are not very clear!
A mysterious electric field somewhere inside the inductor! Where did that come from?
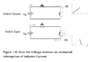
It turns out, that according to Lenz and/or Faraday, the current takes time to build up in an inductor only because of ‘induced voltage.’ This voltage, by definition, opposes any external effort to change the existing flux (or current) in an inductor. So if the current is fixed, yes, there is no voltage present across the inductor, it then behaves just as a piece of conducting wire. But the moment we try to change the current, we get an induced voltage across it. By definition, the voltage measured across an inductor at any moment (whether the switch is open or closed) is the ‘induced voltage.’
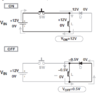
So let us now try to figure out exactly how the induced voltage behaves when the switch is closed. Looking at the inductor charging phase, the inductor current is initially zero. Thereafter, by closing the switch, we are attempting to cause a sudden change in the current. The induced voltage now steps in to try to keep the current down to its initial value(zero).
So we apply ‘Kirchhoff’s voltage law’ to the closed loop in question. Therefore, at the moment the switch closes, the induced voltage must be exactly equal to the applied voltage, since the voltage drop across the series resistance R is initially zero (by Ohm’s law).
As time progresses, we can think intuitively in terms of the applied voltage “winning.” This causes the current to rise up progressively. But that also causes the voltage drop across R to increase, and so the induced voltage must fall by the same amount (to remain faithful to Kirchhoff’s voltage law).
That tells us exactly what the induced voltage (voltage across inductor) is during the entire switch-closed phase.
Why does the applied voltage “win”? For a moment, let’s suppose it didn’t. That would mean the applied voltage and the induced voltage have managed to completely counter-balance each other — and the current would then remain at zero. However, that cannot be, because zero rate of change in current implies no induced voltage either! In other words, the very existence of induced voltage depends on the fact that current changes, and it must change.
We also observe rather thankfully, that all the laws of nature bear each other out. There is no contradiction whichever way we look at the situation. For example, even though the current in the inductor is subsequently higher, its rate of change is less, and therefore, so is the induced voltage (on the basis of Faraday’s/Lenz’s law). And this “allows” for the additional drop appearing across the resistor, as per Kirchhoff’s voltage law!