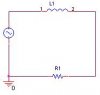
I read that when a motor needs reactive power, it is not necessary to go all the way back to electric power generators on the transmission grid to get it, because you can simply put a capacitor at the location of the motor and it will provide the VARs needed by the motor.
If we treat the motor as an inductor, then without the capacitor we receive a RL circuit:
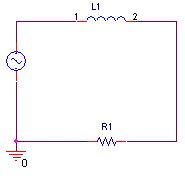
How is it suggested to connect the capacitor?
If you connect the capacitor in parallel to the RL, then you'd increase the current drawn from the power line, since (R+XL) < (R+XL)||XC, and would therefore increase the reactive power supplied by the power grid, so I dont see how it helped.
If we treat the motor as an inductor, then without the capacitor we receive a RL circuit:
How is it suggested to connect the capacitor?
If you connect the capacitor in parallel to the RL, then you'd increase the current drawn from the power line, since (R+XL) < (R+XL)||XC, and would therefore increase the reactive power supplied by the power grid, so I dont see how it helped.