electricity86
New Member
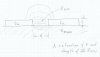
If two traces are close to each other, and in one trace there is suddenly a pulse of voltage, then a capacitance is created between the two traces.
I dont understand why, and what parameters that capacitance's size depends on.
I know that C = I / (dV/dt), C = Aε/d, and that Xc = 1 / (jωc).
I jst dont understand that, and would love some help.
Thank you.
I dont understand why, and what parameters that capacitance's size depends on.
I know that C = I / (dV/dt), C = Aε/d, and that Xc = 1 / (jωc).
I jst dont understand that, and would love some help.
Thank you.