THANX guys for ur assistance with my spice problems 
now i've made and plotted a working circuit, a DC buck convertor, with LTspice and started tweaking it around. But one of the traces on my plot shows a math function that is not producing the right #s and i can't figure out why. The current thru R1 is supposed to be equal to the instantaneous average of the current through V2.
The equation for V is the integral of the (green) current thru V2, summed over a Δt of 22u, divided by 22u. So the white trace at the top is supposed to be parallel with the green one underneath. And at the beginning, it is. But the deviation looks very linear, like there's some kind of bias goin on in B1. I have zoomed in systematically at each 10ms interval and compared the average of the two traces. the top one is definitely deviating and has the wrong slope. anyone know what the problem could be?
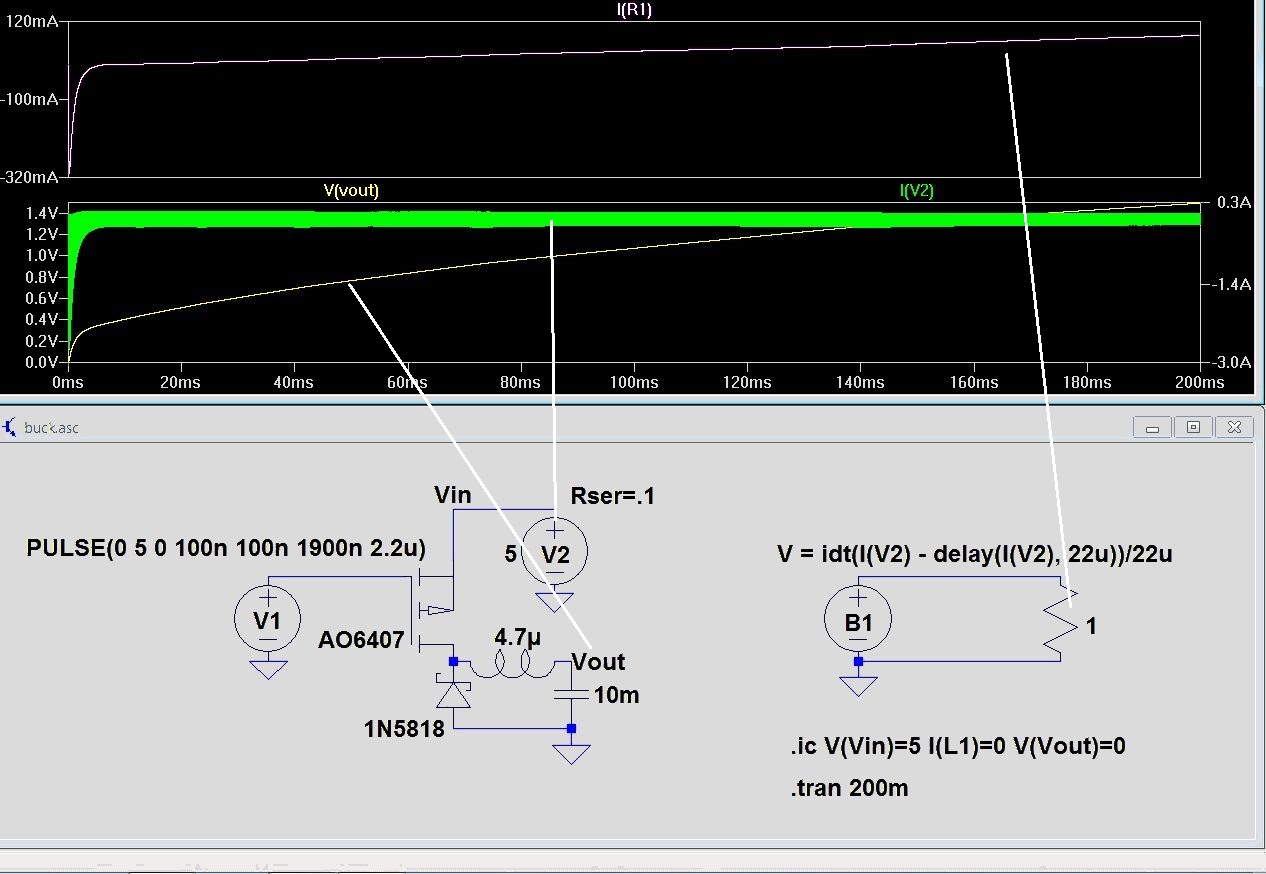
now i've made and plotted a working circuit, a DC buck convertor, with LTspice and started tweaking it around. But one of the traces on my plot shows a math function that is not producing the right #s and i can't figure out why. The current thru R1 is supposed to be equal to the instantaneous average of the current through V2.
The equation for V is the integral of the (green) current thru V2, summed over a Δt of 22u, divided by 22u. So the white trace at the top is supposed to be parallel with the green one underneath. And at the beginning, it is. But the deviation looks very linear, like there's some kind of bias goin on in B1. I have zoomed in systematically at each 10ms interval and compared the average of the two traces. the top one is definitely deviating and has the wrong slope. anyone know what the problem could be?

