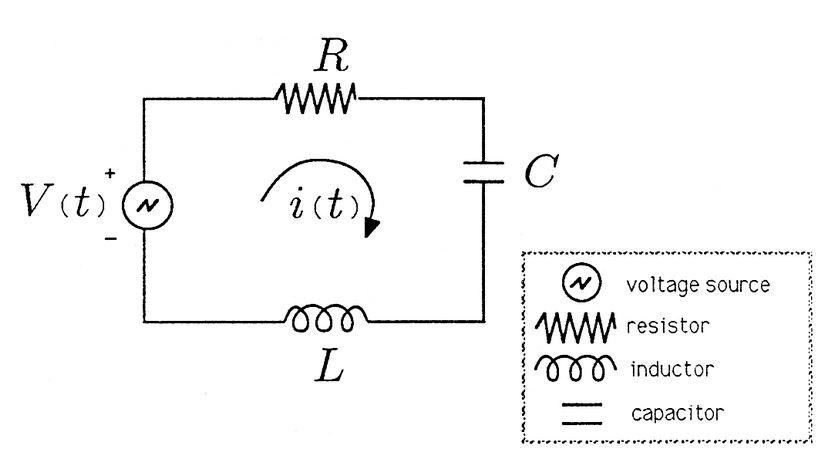
Hello again,
Your second question reveals why this doesnt make sense to you i think. Lets see if this helps...
For your first question, you wrote:
Why this works: f(x+y)=f(x)+f(y)
but that's not really the question you should be asking if you knew the answer to your second question, i think. You would have instead asked this:
Why this works: f(0.5*(x+x'))=f(0.5*x)+f(0.5*x') where x' is the complex conjugate of x.
So maybe now you have already guessed what is coming next

e^-j(wt+θ) is the complex conjugate of e^j(wt+θ) , and that should answer your second question.
So as i said in my previous post, the imaginary parts cancel out in the final operation so we only get the real part remaining, and this is equivalent to using just one of the two and then later taking the real part of the total result. And just to make this clear, when we take the real part of the total result that means we just cancel the imaginary part almost like pretending it isnt there anymore. An example is for X=a+bj:
Real(a+bj)=a
so the real part is just 'a'. This is equivalent to adding the guts to the complex conjugate of the guts and then dividing by 2.
So i think your main problem is that you are viewing the two terms as exponential as in e^iX so it is harder to see the relationships but instead you should be looking at the Euler equivalents:
e^ix=cos(x)+i*sin(x)
e^-ix=cos(x)-i*sin(x)
and from this we can easily see that they are the complex conjugates of each other. Replace 'x' with wt+θ and you get the identities you want.
We then also see that we have these identities:
f(0.5*(x+x'))=Real(f(x))
f(0.5*(x+x'))=Real(f(x'))
and to be complete:
Real(f(x))=Real(f(x'))