Fg limit frequency calculation. Active band-pass filter

[Relay221]

hi I need help with calculating the cutoff frequency Fg. There are several formulas, but I don't know which one to use because every time I get out a different value in (Hz).

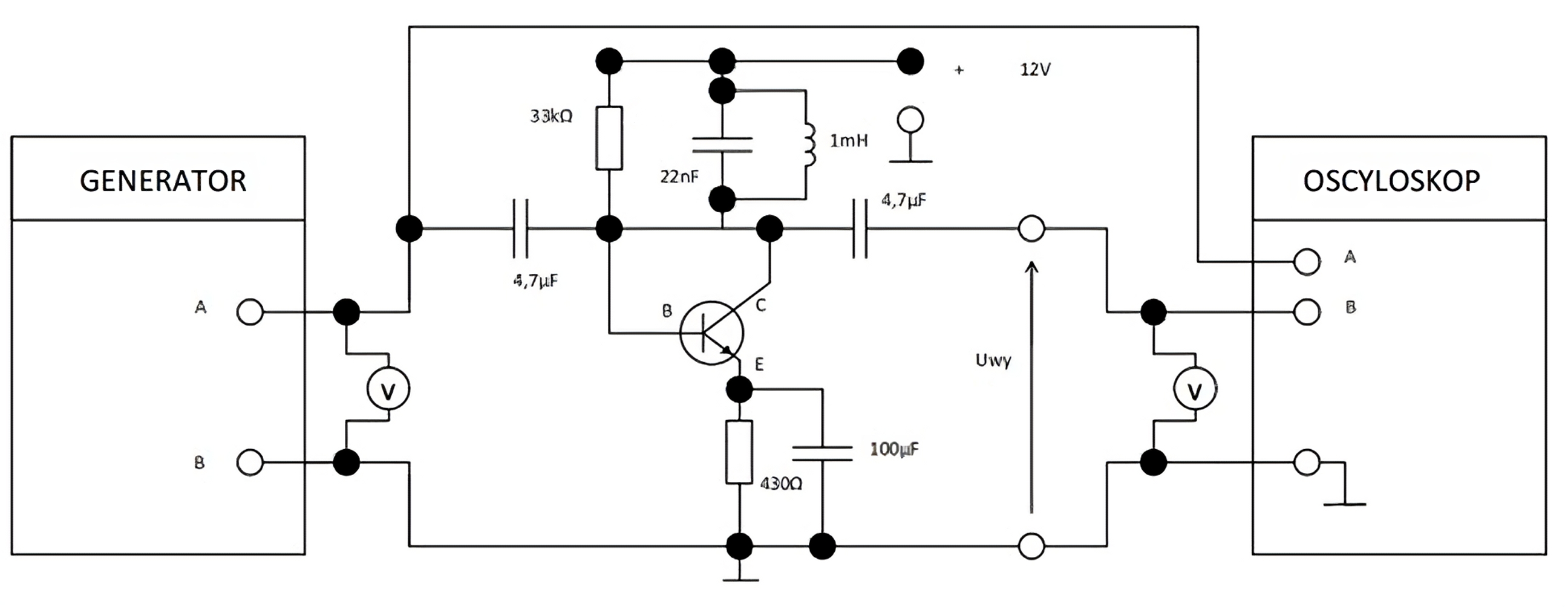
Below is the schematic of this filter (active band pass filter) + its characteristics.

I care about the correct solution If I misunderstand something or there is an error in the diagram in the characteer please correct me

characteristics (calculated using excel):

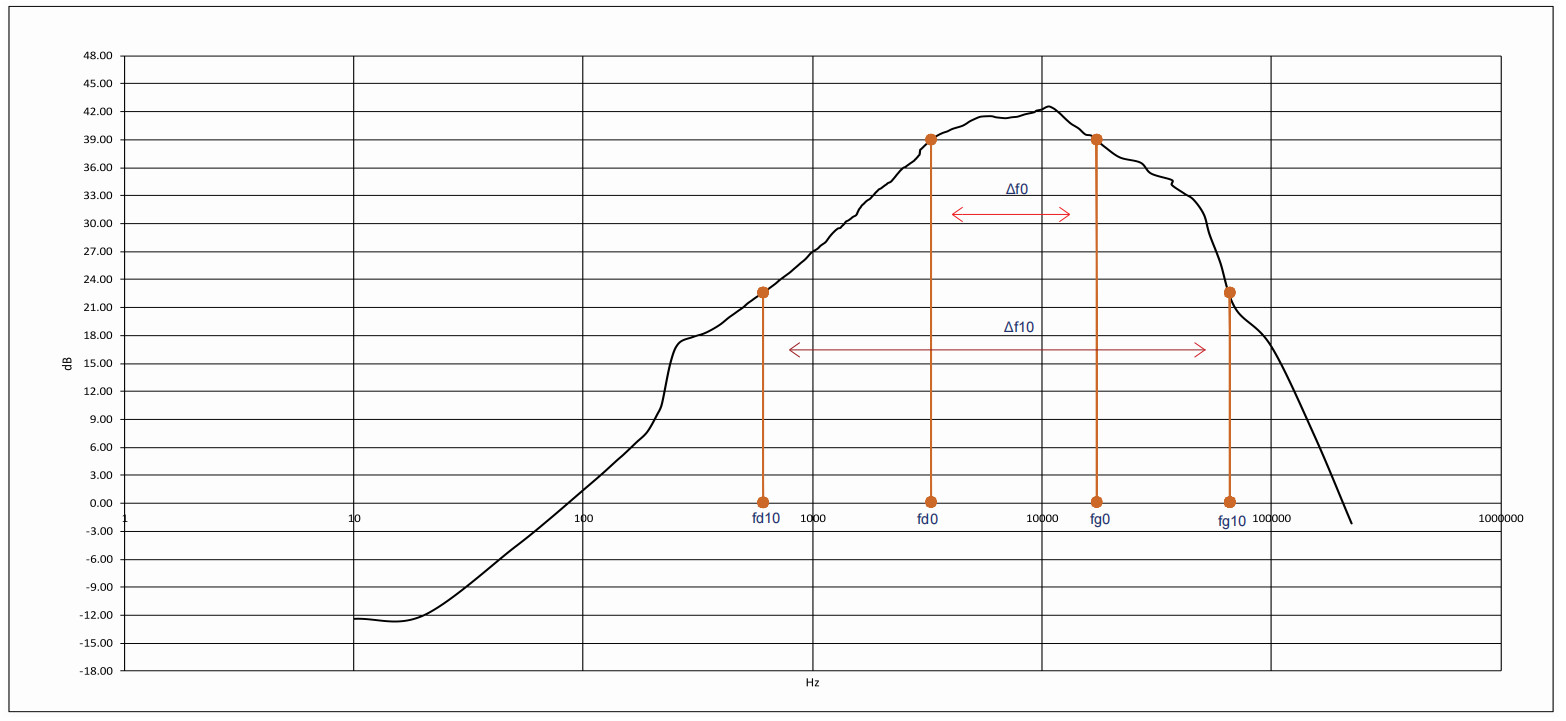
I am not 100% sure about what I drew , but it seems to me that there is a fmeasure otherwise fg but it is calculated with the value of delta f0 or delta f10 from the characterization . I marked fmeasure for -3dB delta f0 and -20 dB delta f10 .

But I still need fcalc (calculated from the formula to later calculate the percentage of measurement error) And from what I tried I got the formula in school . fcalc=1/(2π√LC) but it seems that the formula is not correct or I don't know how to calculate it . Using chat gpt I found out that there is a formula Fg= fl+fh/2 Where fg is the cutoff frequency,fL is the lower cutoff frequency, and fH is the upper cutoff frequency . I don't know if the formula is correct and I did everything right but please correct me if necessary

 

[rjenkinsgb]

You appear to have a stray connection in the diagram - it shows the base & collector (input and output) directly linked??

fcalc=1/(2π√LC) is the correct formula, with the capacitance in Farads and the inductance in Henries - so the capacitance is 22E-9 Farads and the inductance 0.001 Henries

I get it to 33,932 Hz.

The filter "slope" depends on the overall "Q" (quality factor) of the tuned circuit. It's fairly heavily loaded, assuming the base to collector link should be removed?? - so not all that high Q, I'd expect?

 

[danadak]

 

[crutschow]

That's not an active filter, as they have negative feedback through the frequency dependent network to sharpen the response.
Yours is just a passive LC filter with gain.

 

[Relay221]

yes the diagram was wrong there should be no connection there thanks for pointing it out

 

[Relay221]

Correct schematic

 

[danadak]

Is it an active filter or is it not ?

If I put that circuit in a black box, and just look at input and output
I see there is a change in amplitude and phase. Keep in mind we have
Z transformations of the bipolar throwing stuff in parallel with the LC
in the collector, so the active part modified the passive part. Sounds
like an active filter to me. But then like Crustchow I usually think of active
as the reactive components are part of a fdbk loop. But if I go on web
looking for a definition I find pretty imprecise definitions of same. Note
we can have G in a passive network, but not Power G.

It does fit the definition, also, of a filter.

Take your pill Dana......


Regards, Dana.

 

[Nigel Goodwin]

Is it an active filter or is it not ?

I would say not - it's basically just a (fairly poor) tuned amplifier, similar to an IF amplifier stage from the 1960's (and earlier). He just needs to make the coil a transformer, add a suitable tap on the primary, bias it decently, and use sensible capacitor values Then it will work fairly well.

 

[danadak]

One of the classic topologies, no - fdbk with reactive elements in fdbk path is :

The one transistor circuit has :

1) Has active element in it
2) Changed signal amplitude
3) Changed signal phase
4) Changed freq response

Sure looks like its active and a filter.....or an "active filter"......

Could we replace the OpAmp follower in above circuit with a emitter follower and then it becomes active ?

Active filter nomenclature police, where you be ?


Regards, Dana.

 

[rjenkinsgb]

I agree with Nigel.

The "filter" part is just a tuned circuit, which is unchanged by the removal of the preamp feeding it - LC tuned circuits can be used prior to amplification, such as in radio receiver front ends.

The preamp does not change how the filter itself works.

 

[JimB]

I agree with Nigel and RJ, it is a badly biased common emitter amplifier with a tuned circuit in the collector.

Active filter? - no I don't think so.

JimB

 

[danadak]

But then we have this :

https://prism.ucalgary.ca/server/api/core/bitstreams/a126904e-b67f-488d-b373-6865d6aa4412/content

Single Transistor Active Filters: What is Possible and What is Not

This paper systematically investigates the design of single transistor second-order active filters out-lining all possible architectures and possible impedance settings using an exhaustive MAPLE search code for all stable cases with the minimum number of passive elements (two resistors and two...

ieeexplore.ieee.org

https://annas-archive.org/scidb/10.1109/TCSI.2014.2332249?scidb_verified=1

https://www.researchgate.net/publication/318013550_RF_and_Microwave_Filter_Design_By_Means_of_Single_Transistor_Active_Inductor_a_Review

Active filter? - yep I think so.


Regards, Dana.

 

[rjenkinsgb]

Either the LC circuit is within the feedback loop, or they are listed as "Second order" which the LC circuit on its own is not??

Either way, it appears the overall filter properties (and not just gain) would be changed without the transistor?

 

[danadak]

Either the LC circuit is within the feedback loop, or they are listed as "Second order" which the LC circuit on its own is not??

The LC is a second order, 2 poles.

Either way, it appears the overall filter properties (and not just gain) would be changed without the transistor?

Correct, a passive LC versus OpAmp RC BPF versus single G element (transistor) all exhibit differing
characteristics. The OpAmp solutions typically contribute themselves 1 - 2 poles, device selected so
that internal poles are far away from filter desired pole locations on root-locus. There are designs
that use those poles to make capacitor-less active filters, but sensitivities can be quite high. The Transistor
contributes more design inflexibility, so effects response even greater. Many IEEE papers on these topics.

A capacitorless bandpass filter using operational amplifier pole - Search - Anna’s Archive

annas-archive.org

Regards, Dana.

 

[Tony Stewart]

An amplifier with frequency selective gain is an active filter in my books.

There will be significant problems trying to build an active LC BPF with a Q of 1000 as in this case, with 130 ohms reactance even if damped by a load R of 10k with a BW of a few Hz. Then other poles come into play for the HPF and real DCR, ESR will affect the result as well as the coupling caps. The thermal stability of fo will also be poor and drift well beyond the BW.

 

[Relay221]

Hi, I see you are wondering if this is an active filter, in school I was told that it is an active filter because it has an active element, in this case a transistor. My question was how to calculate Fcalc (cutoff frequency) and whether the formula that RJ wrote is correct to calculate fg. From the characteristics I drew, it seems to me that the cutoff frequency can be calculated from the difference between fd0 and fg0 or delta f0 .Is this correct? I'm wondering if I'm making a mistake somewhere, because fcalc and fmeasure should supposedly agree to some extent, obviously with measurement and calculation error

 

[Tony Stewart]

Hi, I see you are wondering if this is an active filter, in school I was told that it is an active filter because it has an active element, in this case a transistor. My question was how to calculate Fcalc (cutoff frequency) and whether the formula that RJ wrote is correct to calculate fg. From the characteristics I drew, it seems to me that the cutoff frequency can be calculated from the difference between fd0 and fg0 or delta f0 .Is this correct? I'm wondering if I'm making a mistake somewhere, because fcalc and fmeasure should supposedly agree to some extent, obviously with measurement and calculation error

fo = 1/(2π√(LC)) is correct.
Q= fo/3dB BW also ratio of R/reactance

 

[Relay221]

Thanks everyone for your help

 

[Tony Stewart]

Did you understand how to choose the unknown variable in this 4D plot?

How about Q is the ratio = real/reactive impedance for parallel L||C and reactive/real for L+C series resonance?

This may be used for low pass filters LPF, high pass HPF , 2nd order bandpass filters BPF or notch filters.