Control Theory: Analysis Stability

[Johnmcfly]

Hello everyone !

At the moment, I am working on a control theory topic and I have a question is related to stability. I know it is a really important topic in control theory.

My question is how to analysis a closed loop system according to a controller.
Let's consider a standard loop like this :

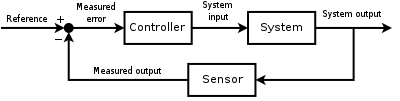
Let's say tha the transfer function for a sensor is equal to 1 (do not know why but always like this).
The system can be a first order system and the controller a PI controller.

What is the approach to determinate the stability and the limits of the system ?

My guess is the following:
- check first the stability of the system (Nyquist plot or Bode)
- check the stability of the system + controller (Nyquist plot or Bode)
- check the stability of the system + controller+feedback (Nyquist plot or Bode)

and for the controller, how should I proceed ? I cannot test for every values of P and I...

Thanks for your feedback !

 

[crutschow]

There's no particular need to do a test of the controller by itself.
The other tests should be sufficient.

 

[Mikebits]

I don't know if this will help, but I recently came across this video series by Analog Devices, have not viewed it though:

 

[Mikebits]

Side note: I just watched the first few videos (short), and they are quite good, but short (

 

[rhaeg]

A possible way to study stability of a control loop is by studying the poles of the the transfer function of the system, this is a fast and easy approach, but not 100%.

However, this approach allows to study the BIBO stability of the system only,
if the system is BIBO stable then it is also Internally stable.
However, if the BIBO is not stable, it may yet be Internally stable, so further checks are required.

All of this is true if we assume the system is Minimal, i.e, there are no zero/pole cancellation.


A more comprehensive approach would be to study the Nyquist plot of the open loop function.