Contradict reasoning in dc-dc converter

[hanhan]

I am reading **broken link removed** from **broken link removed**site. I am uncomfortable with the part Two Flaws of Uncompensated PCMC.
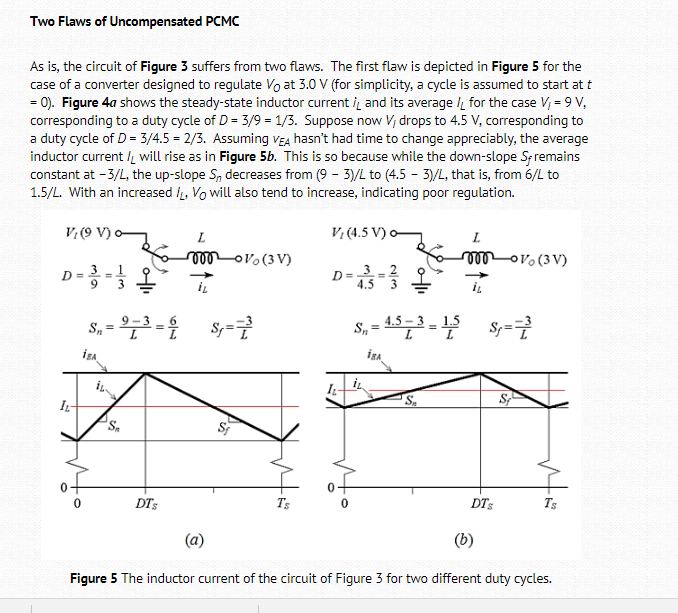
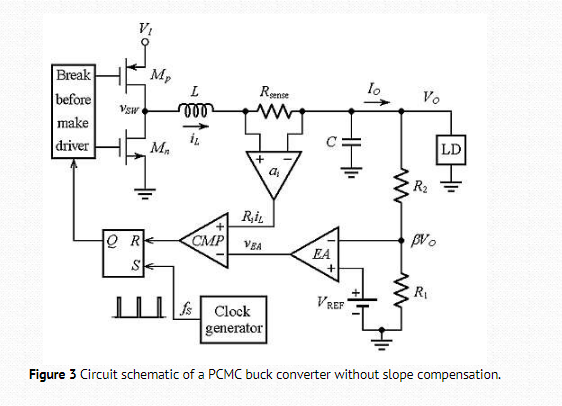
The explanation seems to be contradict with each other.

Please look at the description below.
Here is the author's reasoning:

First for the case VI = 9 V, Vo = 3V, corresponding to a duty cycle of D = 3/9 = 1/3.
Now assuming that VI drop to 4.5V, Vo remaining 3V and new duty cycle D = 3/4.5 = 2/3. Also assuming that vEA hasn’t had time to change appreciably.
Then this results in average inductor current iL increases.
However average inductor current increases means that Vo should increase. With an increased IL, VO will also tend to increase, indicating poor regulation.

This seems to be contradict. The author assumed that Vo constant but that assumption leads to increasing of Vo. So this only means that the initial assumption is not correct. And we can not use that assumption to make any conclusion whether the converter indicates poor regulation or not.
Is there something obvious I am missing here?

When Vin drops and duty cycle increases correspondingly the average inductor current keeps constant and only inductor ripple decreases. How does that indicates poor regulation?

 

[ronsimpson]

When Vin drops and duty cycle increases correspondingly the average inductor current keeps constant and only inductor ripple decreases. How does that indicates poor regulation?

It has been many years. I do not read about this I just do it. So I may be wrong.
Voltage mode = no need for slope comp.
Current mode with less than 50% on time = no need.

The way I see it;
Fig 5 ...9V The saw tooth is inside the error amplifier loop. (it is part of the gain)
Fig5 ...4.5V The saw tooth is much smaller making the gain higher. As the input voltage goes down the slope approaches zero and the gain approaches infinity. (this is not a stable situation)
It is very difficult to make a stable power supply when the gain changes with input voltage.
If that is hard to see; think about Vin of 3.001 volts. So a variation of 0.001V will for the duty cycle to change from 0 to 100%.

 

[dknguyen]

It doesn't sound like a contradiction to me. He never says the voltage is constant.

I think the confusion might be coming from the fact you seem to be thinking that current ripple is directly equivalent to voltage regulation or voltage ripple.

If my definitions are correct, even though voltage ripple and voltage regulation are both voltages, they're considered separately. The metric for regulation isn't concerned about the ripple. It's only concerned about the average.

 

[hanhan]

It has been many years. I do not read about this I just do it. So I may be wrong.
Voltage mode = no need for slope comp.
Current mode with less than 50% on time = no need.

The way I see it;
Fig 5 ...9V The saw tooth is inside the error amplifier loop. (it is part of the gain)
Fig5 ...4.5V The saw tooth is much smaller making the gain higher. As the input voltage goes down the slope approaches zero and the gain approaches infinity. (this is not a stable situation)
It is very difficult to make a stable power supply when the gain changes with input voltage.
If that is hard to see; think about Vin of 3.001 volts. So a variation of 0.001V will for the duty cycle to change from 0 to 100%.

The first part you got it correctly.
However for the part relating to figure 5, I am not sure what you meant by sawtooth here. Did you mean the compensation sawtooth?

 

[hanhan]

It doesn't sound like a contradiction to me. He never says the voltage is constant.

I think the confusion might be coming from the fact you seem to be thinking that current ripple is directly equivalent to voltage regulation or voltage ripple. It's not. Voltage ripple is not even considered to be part of voltage regulation accuracy (voltage regulation is the average voltage).

It doesn't sound like a contradiction to me. He never says the voltage is constant.

That is not the contradiction I meant to say. What I said above is that he used the assumption that Vout is constant and then based on that to infer inductor current increases.
The increasing of inductor current results in Vout increases.
So this means the initial assumption that Vout is constant is not correct.
So he cannot make any conclusion that is result of the constant output voltage assumption because the assumption is not correct.

Also, why did he get average inductor current increases like that? In reality, when Vin drop, Vout remains the same then average inductor current should remains the same.
Can you explain why the first problem he meant to say?

 

[dknguyen]

That is not the contradiction I meant to say. What I said above is that he used the assumption that Vout is constant and then based on that to infer inductor current increases.
The increasing of inductor current results in Vout increases.
So this means the initial assumption that Vout is constant is not correct.
So he cannot make any conclusion that is result of the constant output voltage assumption because the assumption is not correct.

Also, why did he get average inductor current increases like that? In reality, when Vin drop, Vout remains the same then average inductor current should remains the same.
Can you explain why the first problem he meant to say?

And I'm saying that he never made the initial assumption that Vout is constant. I don't see that assumption anywhere in the article.

That increase in current is a little weird. It makes sense when you look at the equations but if you're talking about a physical explanation, I'm still staring at it.

EDIT: I think it's because it takes time for the error amplifier to react and since the input voltage is now, closer to the output voltage it causes the average current to become higher but less ripple.

 

[hanhan]

And I'm saying that he never made the initial assumption that Vout is constant. I don't see that assumption anywhere in the article.

He didn't say it directly but he used it several times in his reasoning. First in calculating duty cycle, second in assuming that down-slope Sf remains constants at -3/L. Also you can easily see it by looking at the figure.

As is, the circuit of Figure 3 suffers from two flaws. The first flaw is depicted in Figure 5 for the case of a converter designed to regulate VO at 3.0 V (for simplicity, a cycle is assumed to start at t= 0). Figure 4a shows the steady-state inductor current iL and its average IL for the case VI = 9 V, corresponding to a duty cycle of D = 3/9 = 1/3. Suppose now VI drops to 4.5 V, corresponding to a duty cycle of D = 3/4.5 = 2/3. Assuming vEA hasn’t had time to change appreciably, the average inductor current IL will rise as in Figure 5b. This is so because while the down-slope Sf remains constant at –3/L, the up-slope Sn decreases from (9 – 3)/L to (4.5 – 3)/L, that is, from 6/L to 1.5/L. With an increased IL, VO will also tend to increase, indicating poor regulation

 

[dknguyen]

He didn't say it directly but he used it several times in his reasoning. First in calculating duty cycle, second in assuming that down-slope Sf remains constants at -3/L. Also you can easily see it by looking at the figure.

View attachment 111471

Those are just approximations, rather than rigorous assumptions, to make things simpler to handle. This is definitely the case with the duty cycle calculation where it is for steady-state conditions which is NOT the same thing as outright being constant. Maybe someone more experienced than me can chime in.

 

[ronsimpson]

I am not sure what you meant by sawtooth here.

In the voltage mode PWM that I use there is an saw tooth oscillator. (0 to 3V) The output of the error amplifier and the voltage saw tooth ramp are compared to make the duty cycle. If the output of the error amp was 1.5V then the dc=50%.

In current mode the oscillator keeps the frequency constant but its ramp is not used. The current ramp is used to set the duty cycle. The output of the error amp is compared against the current ramp in the inductor (or transistor). Because the current ramp changes with input/output voltage it effects many things. (some in a good way and some in a bad way of the duty cycle is high)

Slope compensation is a way of combining the current ramp and the voltage ramp to get the effects of current mode and voltage mode.

 

[hanhan]

Those are just approximations, rather than rigorous assumptions, to make things simpler to handle. This is definitely the case with the duty cycle calculation where it is for steady-state conditions which is NOT the same thing as outright being constant. Maybe someone more experienced than me can chime in.

That kinds of approximation makes me confused than not. I really don't know what and why the first flaw happens while reading this part of the article.

 

[hanhan]

In the voltage mode PWM that I use there is an saw tooth oscillator. (0 to 3V) The output of the error amplifier and the voltage saw tooth ramp are compared to make the duty cycle. If the output of the error amp was 1.5V then the dc=50%.

In current mode the oscillator keeps the frequency constant but its ramp is not used. The current ramp is used to set the duty cycle. The output of the error amp is compared against the current ramp in the inductor (or transistor). Because the current ramp changes with input/output voltage it effects many things. (some in a good way and some in a bad way of the duty cycle is high)

Slope compensation is a way of combining the current ramp and the voltage ramp to get the effects of current mode and voltage mode.

I understand this basics but confused by the first flaw that he mentioned in the article. Did he mean that the circuit in figure 3 is the uncompensated circuit? If so, why the first flaw happens?