Hey, I wanted to ask a few questions please regarding Boost Converter.
1.When the switch is close, the current increases linearly.
When the switch opens, the inductor's voltage jumps from zero to a peak value that will cause a voltage drop on the diode so the diode's current will equal the inductor's current, is it correct?
2. Every time the switch closes, the inductor gains current, and when the switch opens, the current flows mostly through the capacitor, assuming that 1/(ωC) < Load_impedance.
So how come the capacitor's voltage doesnt keep growing?
3. I suppose that the diode is needed there in order for the capacitor not to discharge into ground when the switch closes. is there any other reason for the diode to be connected there?
Thank you very much.
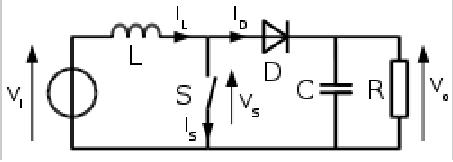
1.When the switch is close, the current increases linearly.
When the switch opens, the inductor's voltage jumps from zero to a peak value that will cause a voltage drop on the diode so the diode's current will equal the inductor's current, is it correct?
2. Every time the switch closes, the inductor gains current, and when the switch opens, the current flows mostly through the capacitor, assuming that 1/(ωC) < Load_impedance.
So how come the capacitor's voltage doesnt keep growing?
3. I suppose that the diode is needed there in order for the capacitor not to discharge into ground when the switch closes. is there any other reason for the diode to be connected there?
Thank you very much.
Attachments
Last edited:

