The Electrician
Active Member
Audio transformers seem to often raise the question of what is the impedance rating of the various windings, and what determines those impedances? How can we measure the rated impedances?
Discussion of the impedance transforming properties of transformers can be found in many textbooks and many web sites, but I'll review certain aspects of those properties especially contrasting the differences between the behavior of ideal transformers compared to the behavior of real transformers.
Let's only consider a transformer with two windings, an audio output transformer with a relatively high impedance rated primary and low impedance rated secondary. If the transformer were ideal, it would have infinite inductance primary and secondary and no losses and no distributed capacitances causing self-resonances.
We could almost make such a thing if the windings were made or room temperature super conducting wire, and if the core material were magnetic unobtainium having infinite permeability and no hysteresis or eddy current losses. We would still have distributed capacitances, though, but I'll ignore the losses from real dielectrics.
Suppose we wanted our transformer to have a 5000 ohm rated primary and 8 ohm rated secondary. Then we would need a turns ratio of 25 to 1; denote that as Nt and let the impedance ratio be Zt = Nt*Nt. We could wind the primary with 250 turns and the secondary with 10 turns (of superconducting wire).
When we discuss impedances connected to or measured at a winding, the measurement will be made with an AC signal of some moderate audio frequency, typically 1 kHz.
Now, we know that if we connect a load of RL ohms to the secondary and measure the impedance at the primary, we would expect to measure Zt*RL ohms. So, for a secondary load impedance of 8 ohms, we would measure 5000 ohms at the primary; for a secondary load of 80 ohms, we would measure 50,000 ohms at the primary. For a secondary load of .8 ohms, we would measure 500 ohms at the primary. This is all with the ideal transformer.
What if we connected a load impedance ZL of zero ohms (a short circuit) to the secondary? The expected primary impedance would be Zt*zero = zero ohms. A short on the secondary would be reflected as a short (zero ohms impedance) on the primary; remember, we are still talking about the behavior of an ideal transformer.
If we connect a load impedance of infinite ohms to the secondary, we would expect to measure Zt*? = ? ohms at the primary with the secondary open circuited. This is in accord with the infinite inductance our ideal transformer would have at both its windings.
So, we can expect that as the load impedance connected to the secondary ranges from zero ohms (a short) to ? ohms (open circuit), the primary impedance will also range from zero to ?. In other words, the primary impedance can have any value at all.
What about the behavior of a real transformer? Such a transformer will be wound with wire which is not super conducting, so it will have resistance. The core material won't have infinite permeability, so the winding inductances won't be infinite; the core material will have finite hysteresis and eddy current losses. The transformer model as presented in the transformer references I mentioned at the beginning will have a series resistance representing the copper losses, and a shunt resistance representing the core losses.
These losses will modify the impedances seen at the primary for various loadings on the secondary. For example, when the secondary has a zero ohms load (a short), the impedance seen at the primary will be increased by the resistance of the primary wire plus the reflected value of the secondary wire resistance; the primary impedance won't be zero ohms with a short on the secondary as it was with the ideal transformer.
When the load on the secondary is infinite ohms (open circuit), the primary impedance won't be ? because the equivalent shunt resistance representing the core loss will be in parallel with the reflected value of the infinite secondary load, giving a value just equal to the shunt equivalent of the core loss.
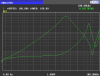
To see all this in action, I've taken a small output transformer with a 5k ohm rated primary impedance and an 8 ohms rated secondary impedance and measured the primary impedance with an open circuit on the secondary, and with a short on the secondary. The primary impedance magnitude was measured with an impedance analyzer from a low frequency of 4 Hz to a high frequency of 100 kHz. The impedance magnitudes are plotted on a log-log graph with 4 Hz at the left edge and 100 kHz at the right edge; major vertical lines are at 10 Hz, 100 Hz, 1 khz and 10 kHz. The impedance scale goes from 100 ohms at the bottom edge of the plot to 100k ohms at the top, with major horizontal lines at 1k and 10k ohms. This plot is shown in the attachment.
The top green curve is the primary impedance with the secondary open circuited (Zoc), and the bottom green curve is the primary impedance with the secondary shorted (Zsc).
The primary impedance can't be any greater than the top curve, no matter what impedance is connected to the secondary, and also can't be any less than the bottom curve no matter what impedance is connected to the secondary. In other words, the impedance we measure at the primary must always fall between the two green curves (up to 20 kHz or so), whatever resistive load we connect to the secondary (capacitive loads can cause the impedance to go a little above the upper green curve, but I'm not getting into that now).
We see that starting at the left side, the upper curve rises as frequency increases. This is because with the secondary open circuited, we are getting no transformer action, and we are just measuring the finite inductance of the primary, whose impedance increases with increasing frequency, as inductors do. Eventually we reach the self-resonance frequency of the primary at about 3 kHz, and then the open circuit impedance begins to decrease with increasing frequency, because the impedance is now capacitive. This is one of the limitations of a real transformer versus an ideal one.
The maximum impedance occurs at the first parallel resonance of the primary winding, but we see that there are more resonances at higher frequencies; for example, the first series resonance, giving an impedance minimum occurs at about 48 kHz.
The lower curve which is the primary impedance with the secondary shorted starts out at about 300 ohms at 4 Hz, and is nearly flat until about 1 kHz where it starts to rise due to the leakage inductance. We see a couple of resonances at higher frequencies. Since the secondary load impedance can't be less than zero ohms (we won't consider negative resistances), the primary impedance must always fall above the lower green curve up to about 20 kHz.
Unlike the ideal transformer which can be used with any value of secondary impedance, this real transformer can't have a primary impedance of greater than about 21k ohms at 1 kHz. This means that if we connected a secondary impedance of 64 ohms, the ideal transformer would transform that to a primary impedance of 40k ohms, but the real transformer just couldn't do that. The real transformer's primary impedance can't be more than about 21k ohms at 1 kHz; the real transformer's ability to transform impedances is limited by its losses.
This defect doesn't just kick in at a primary impedance of about 20k ohms; as soon as you move away from the optimum primary impedance of 5k ohms, the effect begins to occur. I'll discuss more in the next post.
Discussion of the impedance transforming properties of transformers can be found in many textbooks and many web sites, but I'll review certain aspects of those properties especially contrasting the differences between the behavior of ideal transformers compared to the behavior of real transformers.
Let's only consider a transformer with two windings, an audio output transformer with a relatively high impedance rated primary and low impedance rated secondary. If the transformer were ideal, it would have infinite inductance primary and secondary and no losses and no distributed capacitances causing self-resonances.
We could almost make such a thing if the windings were made or room temperature super conducting wire, and if the core material were magnetic unobtainium having infinite permeability and no hysteresis or eddy current losses. We would still have distributed capacitances, though, but I'll ignore the losses from real dielectrics.
Suppose we wanted our transformer to have a 5000 ohm rated primary and 8 ohm rated secondary. Then we would need a turns ratio of 25 to 1; denote that as Nt and let the impedance ratio be Zt = Nt*Nt. We could wind the primary with 250 turns and the secondary with 10 turns (of superconducting wire).
When we discuss impedances connected to or measured at a winding, the measurement will be made with an AC signal of some moderate audio frequency, typically 1 kHz.
Now, we know that if we connect a load of RL ohms to the secondary and measure the impedance at the primary, we would expect to measure Zt*RL ohms. So, for a secondary load impedance of 8 ohms, we would measure 5000 ohms at the primary; for a secondary load of 80 ohms, we would measure 50,000 ohms at the primary. For a secondary load of .8 ohms, we would measure 500 ohms at the primary. This is all with the ideal transformer.
What if we connected a load impedance ZL of zero ohms (a short circuit) to the secondary? The expected primary impedance would be Zt*zero = zero ohms. A short on the secondary would be reflected as a short (zero ohms impedance) on the primary; remember, we are still talking about the behavior of an ideal transformer.
If we connect a load impedance of infinite ohms to the secondary, we would expect to measure Zt*? = ? ohms at the primary with the secondary open circuited. This is in accord with the infinite inductance our ideal transformer would have at both its windings.
So, we can expect that as the load impedance connected to the secondary ranges from zero ohms (a short) to ? ohms (open circuit), the primary impedance will also range from zero to ?. In other words, the primary impedance can have any value at all.
What about the behavior of a real transformer? Such a transformer will be wound with wire which is not super conducting, so it will have resistance. The core material won't have infinite permeability, so the winding inductances won't be infinite; the core material will have finite hysteresis and eddy current losses. The transformer model as presented in the transformer references I mentioned at the beginning will have a series resistance representing the copper losses, and a shunt resistance representing the core losses.
These losses will modify the impedances seen at the primary for various loadings on the secondary. For example, when the secondary has a zero ohms load (a short), the impedance seen at the primary will be increased by the resistance of the primary wire plus the reflected value of the secondary wire resistance; the primary impedance won't be zero ohms with a short on the secondary as it was with the ideal transformer.
When the load on the secondary is infinite ohms (open circuit), the primary impedance won't be ? because the equivalent shunt resistance representing the core loss will be in parallel with the reflected value of the infinite secondary load, giving a value just equal to the shunt equivalent of the core loss.
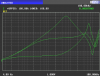
To see all this in action, I've taken a small output transformer with a 5k ohm rated primary impedance and an 8 ohms rated secondary impedance and measured the primary impedance with an open circuit on the secondary, and with a short on the secondary. The primary impedance magnitude was measured with an impedance analyzer from a low frequency of 4 Hz to a high frequency of 100 kHz. The impedance magnitudes are plotted on a log-log graph with 4 Hz at the left edge and 100 kHz at the right edge; major vertical lines are at 10 Hz, 100 Hz, 1 khz and 10 kHz. The impedance scale goes from 100 ohms at the bottom edge of the plot to 100k ohms at the top, with major horizontal lines at 1k and 10k ohms. This plot is shown in the attachment.
The top green curve is the primary impedance with the secondary open circuited (Zoc), and the bottom green curve is the primary impedance with the secondary shorted (Zsc).
The primary impedance can't be any greater than the top curve, no matter what impedance is connected to the secondary, and also can't be any less than the bottom curve no matter what impedance is connected to the secondary. In other words, the impedance we measure at the primary must always fall between the two green curves (up to 20 kHz or so), whatever resistive load we connect to the secondary (capacitive loads can cause the impedance to go a little above the upper green curve, but I'm not getting into that now).
We see that starting at the left side, the upper curve rises as frequency increases. This is because with the secondary open circuited, we are getting no transformer action, and we are just measuring the finite inductance of the primary, whose impedance increases with increasing frequency, as inductors do. Eventually we reach the self-resonance frequency of the primary at about 3 kHz, and then the open circuit impedance begins to decrease with increasing frequency, because the impedance is now capacitive. This is one of the limitations of a real transformer versus an ideal one.
The maximum impedance occurs at the first parallel resonance of the primary winding, but we see that there are more resonances at higher frequencies; for example, the first series resonance, giving an impedance minimum occurs at about 48 kHz.
The lower curve which is the primary impedance with the secondary shorted starts out at about 300 ohms at 4 Hz, and is nearly flat until about 1 kHz where it starts to rise due to the leakage inductance. We see a couple of resonances at higher frequencies. Since the secondary load impedance can't be less than zero ohms (we won't consider negative resistances), the primary impedance must always fall above the lower green curve up to about 20 kHz.
Unlike the ideal transformer which can be used with any value of secondary impedance, this real transformer can't have a primary impedance of greater than about 21k ohms at 1 kHz. This means that if we connected a secondary impedance of 64 ohms, the ideal transformer would transform that to a primary impedance of 40k ohms, but the real transformer just couldn't do that. The real transformer's primary impedance can't be more than about 21k ohms at 1 kHz; the real transformer's ability to transform impedances is limited by its losses.
This defect doesn't just kick in at a primary impedance of about 20k ohms; as soon as you move away from the optimum primary impedance of 5k ohms, the effect begins to occur. I'll discuss more in the next post.