Introduction --
Occasionally it is desired to convert binary numbers to decimal (usually for a decimal readout), or rarely, a decimal number to binary.
Typically the first step for displaying a binary number in a decimal display is to convert the binary number to BCD (Binary Coded Decimal).
(BCD represents each of the decimal digits 0 to 9 by a 4-bit binary number 0000 to 1001.)
This BCD number is then easily decoded into decimal display digits.
Although at first glance it might seem simple to do this conversion with logic, it requires many gates to perform for even a small number of bits.
For example a 5-bit number requires about 30 gates, and the number of gates required increases significantly with the number of bits to convert.
A low parts-count approach is to use a Binary-to-BCD algorithm, such as the Shift-and-Add-3, in a microprocessor, but that requires programming expertise and programming equipment.
Another minimal approach is use a ROM (read only memory) containing a look-up table, but that also requires the ability and equipment to program the device.
There is a 74185 IC that has a built-in pre-programmed ROM to do the conversion, but is an obsolete device that can be expensive and difficult to find.
Counter Conversion Technique--
The approach discussed here uses a combination of standard binary and BCD counters to convert a parallel binary number to the equivalent parallel BCD number (the reverse conversion is discussed later).
The circuit for this is simple, requiring only one D flip-flop plus the number of counters (all identical part number), as determined by the maximum number to be converted (≈2 counters per BCD digit).
If a system clock is not available than a NAND/NOR/INVERTER gate package can be used to build a simple multivbrator clock generator.
The operation of this circuit is straightforward.
The binary counter counts the binary number down to zero, while the BCD counter counts up for the same number of counts.
Thus when the binary counter reaches zero, the equivalent BCD number is available at the BCD counter output.
The frequency of the clock and the magnitude of the number being converted determines how long the conversion process takes, with the number of clock pulses equaling the number being converted.
Thus larger numbers take a longer conversion time, but is still reasonable for a typical number of display digits.
For example, a maximum 6 digit value of 999,999 takes just 500ms with a 2MHz clock, usually sufficient for a visual readout of the number.
Design/Simulation--
The LTspice simulation below, is for a small demonstration circuit that converts binary to two BCD digits of up to 99 counts (28 less than a full 7-bits).
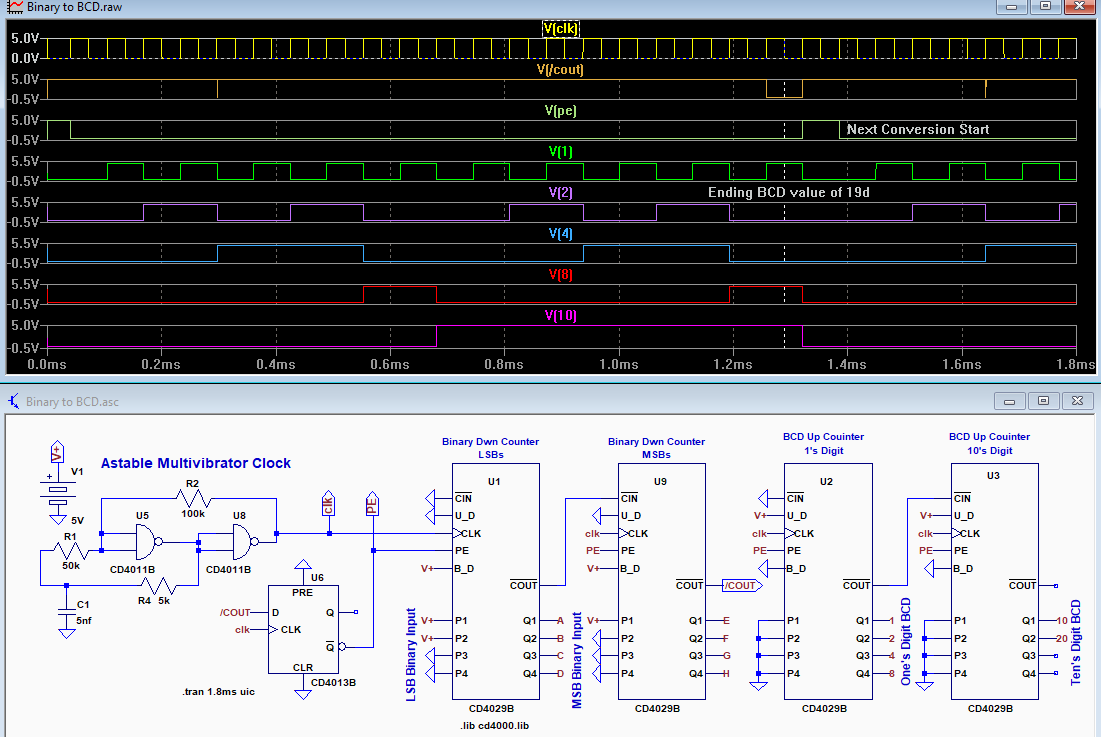
All counters are CD4029's, with U1 & U9 configured as an 8-bit binary down-counter, and U2 & U3 configured as a two digit BCD up-counter.
(So only 7-bits to a maximum value of 99d can be used here).
The binary number is parallel loaded into U1 & U9 from inputs P1-P4 when the PE (Preset Enable) input is momentarily driven high.
(All PE inputs are common, so U2 & U3 are set to zero simultaneous with the U1, U9 load, since their P1-P4 inputs are all zero.)
U1 & U9 then count down to zero, at which point U9's /COUT output goes low.
This signals that the converted BCD number is available at the U2 & U3 Q1-Q4 outputs.
One ↑clock pulse later the counters are preset for the next conversion (↑ = rising edge).
The simulation shows the conversion for a binary input of 10011 (19d).
This is converted to 19 in the BCD output of U2 (V10) & U1 (V1, V2, V4, V8), shown at the vertical dotted marker, where /COUT is low.
(The one's digit 0-9 is in U2 and the ten's digit 0-9 is in U3)
U9-/COUT going low at the D-input of FF U6 causes its /Q output (all PE inputs) to go from low to high at the next ↑clock, setting U1's & U9's counter value to their P1-P4 binary input, and U2-U3 to zero for the next conversion.
U9's /COUT and thus FF's D-input returns high after one clock pulse. The FF /Q output then goes low one ↑clock pulse later, restarting the conversion.
(U1's & U9's binary input is shown as fixed, but normally would be an arbitrary number from a digital source for conversion.)
Clock--
The simulation clock is generated by two NAND gates (U5 & U6) connected as a simple astable multivibrator (NOR or INVERTER gates could also be used).
Its frequency is ≈15.6kHz with the component values shown, as determined primarily by the values R4 & C1. This provides a conversion time of <6.4ms for the maximum binary input of 99d.
The clock frequency is not critical and can be anything up to the maximum clock frequency of the logic family used.
(If an appropriate external clock signal is available from the system, then that can replace the clock circuit shown, eliminating the NAND gate and associated discrete parts,)
Numeric Display--
To show the number, the BCD values from U2 & U3 can be decoded for a decimal display. Most common are ones to drive a 7-segment display from a BCD input.
Note that a latch is needed to capture the BCD value at the end of the conversion (/COUT low) and hold the value steady until the next conversion is finished. This latch is often built into the decoder.
A minimum parts count solution would be to replace U2 & U3 with a decimal counter, such as the the 4026 or 4033, which have the 7-segment decoder built it.
BCD to Binary--
The need for a BCD to Binary conversion is rare, but this circuit can readily do that by reversing just one control pin on each counter (can be done by external logic control if desired).
Change U1 & U9 to a BCD counter (pin B_D to ground). and change U2 & U3 to a binary counter (pin B_D to logic high).
Now inputting a BCD number to the P1-P4 inputs of U1 & U9 will give the binary equivalent at the Q1-Q4 outputs of U2 & U3.
Expansion--
The circuit can be readily expanded by simply cascading the counters to the desired number of bits and/or digits.
For example, adding one BCD counter (3 digits total) will allow the full 8-bit binary count (255) of U1 and U9 to be displayed.
The number of required decimal counters will be ≥ the number of binary counters in an expansion, since a 4-bit binary counter can go to 15, but a 4-bit BCD counter only goes to 9. The average ratio of BCD counters to binary counters is ≈6/5.
The conversion time goes up as determined by maximum number converted (number of clock pulses equals the number converted) so the clock frequency may have to be increased to get the desired conversion time. Two to three conversions per second is usually sufficient for visual displays.
Construction--
Power and ground are not shown for the IC's as well as 100nF ceramic decoupling caps at the IC power pins to ground, which must be added.
Be sure and connect all unused IC inputs to ground or erratic behaviour may occur.
Occasionally it is desired to convert binary numbers to decimal (usually for a decimal readout), or rarely, a decimal number to binary.
Typically the first step for displaying a binary number in a decimal display is to convert the binary number to BCD (Binary Coded Decimal).
(BCD represents each of the decimal digits 0 to 9 by a 4-bit binary number 0000 to 1001.)
This BCD number is then easily decoded into decimal display digits.
Although at first glance it might seem simple to do this conversion with logic, it requires many gates to perform for even a small number of bits.
For example a 5-bit number requires about 30 gates, and the number of gates required increases significantly with the number of bits to convert.
A low parts-count approach is to use a Binary-to-BCD algorithm, such as the Shift-and-Add-3, in a microprocessor, but that requires programming expertise and programming equipment.
Another minimal approach is use a ROM (read only memory) containing a look-up table, but that also requires the ability and equipment to program the device.
There is a 74185 IC that has a built-in pre-programmed ROM to do the conversion, but is an obsolete device that can be expensive and difficult to find.
Counter Conversion Technique--
The approach discussed here uses a combination of standard binary and BCD counters to convert a parallel binary number to the equivalent parallel BCD number (the reverse conversion is discussed later).
The circuit for this is simple, requiring only one D flip-flop plus the number of counters (all identical part number), as determined by the maximum number to be converted (≈2 counters per BCD digit).
If a system clock is not available than a NAND/NOR/INVERTER gate package can be used to build a simple multivbrator clock generator.
The operation of this circuit is straightforward.
The binary counter counts the binary number down to zero, while the BCD counter counts up for the same number of counts.
Thus when the binary counter reaches zero, the equivalent BCD number is available at the BCD counter output.
The frequency of the clock and the magnitude of the number being converted determines how long the conversion process takes, with the number of clock pulses equaling the number being converted.
Thus larger numbers take a longer conversion time, but is still reasonable for a typical number of display digits.
For example, a maximum 6 digit value of 999,999 takes just 500ms with a 2MHz clock, usually sufficient for a visual readout of the number.
Design/Simulation--
The LTspice simulation below, is for a small demonstration circuit that converts binary to two BCD digits of up to 99 counts (28 less than a full 7-bits).
All counters are CD4029's, with U1 & U9 configured as an 8-bit binary down-counter, and U2 & U3 configured as a two digit BCD up-counter.
(So only 7-bits to a maximum value of 99d can be used here).
The binary number is parallel loaded into U1 & U9 from inputs P1-P4 when the PE (Preset Enable) input is momentarily driven high.
(All PE inputs are common, so U2 & U3 are set to zero simultaneous with the U1, U9 load, since their P1-P4 inputs are all zero.)
U1 & U9 then count down to zero, at which point U9's /COUT output goes low.
This signals that the converted BCD number is available at the U2 & U3 Q1-Q4 outputs.
One ↑clock pulse later the counters are preset for the next conversion (↑ = rising edge).
The simulation shows the conversion for a binary input of 10011 (19d).
This is converted to 19 in the BCD output of U2 (V10) & U1 (V1, V2, V4, V8), shown at the vertical dotted marker, where /COUT is low.
(The one's digit 0-9 is in U2 and the ten's digit 0-9 is in U3)
U9-/COUT going low at the D-input of FF U6 causes its /Q output (all PE inputs) to go from low to high at the next ↑clock, setting U1's & U9's counter value to their P1-P4 binary input, and U2-U3 to zero for the next conversion.
U9's /COUT and thus FF's D-input returns high after one clock pulse. The FF /Q output then goes low one ↑clock pulse later, restarting the conversion.
(U1's & U9's binary input is shown as fixed, but normally would be an arbitrary number from a digital source for conversion.)
Clock--
The simulation clock is generated by two NAND gates (U5 & U6) connected as a simple astable multivibrator (NOR or INVERTER gates could also be used).
Its frequency is ≈15.6kHz with the component values shown, as determined primarily by the values R4 & C1. This provides a conversion time of <6.4ms for the maximum binary input of 99d.
The clock frequency is not critical and can be anything up to the maximum clock frequency of the logic family used.
(If an appropriate external clock signal is available from the system, then that can replace the clock circuit shown, eliminating the NAND gate and associated discrete parts,)
Numeric Display--
To show the number, the BCD values from U2 & U3 can be decoded for a decimal display. Most common are ones to drive a 7-segment display from a BCD input.
Note that a latch is needed to capture the BCD value at the end of the conversion (/COUT low) and hold the value steady until the next conversion is finished. This latch is often built into the decoder.
A minimum parts count solution would be to replace U2 & U3 with a decimal counter, such as the the 4026 or 4033, which have the 7-segment decoder built it.
BCD to Binary--
The need for a BCD to Binary conversion is rare, but this circuit can readily do that by reversing just one control pin on each counter (can be done by external logic control if desired).
Change U1 & U9 to a BCD counter (pin B_D to ground). and change U2 & U3 to a binary counter (pin B_D to logic high).
Now inputting a BCD number to the P1-P4 inputs of U1 & U9 will give the binary equivalent at the Q1-Q4 outputs of U2 & U3.
Expansion--
The circuit can be readily expanded by simply cascading the counters to the desired number of bits and/or digits.
For example, adding one BCD counter (3 digits total) will allow the full 8-bit binary count (255) of U1 and U9 to be displayed.
The number of required decimal counters will be ≥ the number of binary counters in an expansion, since a 4-bit binary counter can go to 15, but a 4-bit BCD counter only goes to 9. The average ratio of BCD counters to binary counters is ≈6/5.
The conversion time goes up as determined by maximum number converted (number of clock pulses equals the number converted) so the clock frequency may have to be increased to get the desired conversion time. Two to three conversions per second is usually sufficient for visual displays.
Construction--
Power and ground are not shown for the IC's as well as 100nF ceramic decoupling caps at the IC power pins to ground, which must be added.
Be sure and connect all unused IC inputs to ground or erratic behaviour may occur.
