I was reading about LDO and this came across this page about Barkhausen's criterion for oscillation.
http://lea.hamradio.si/~s53mv/spectana/vco.html
Could you help me with the question in picture?
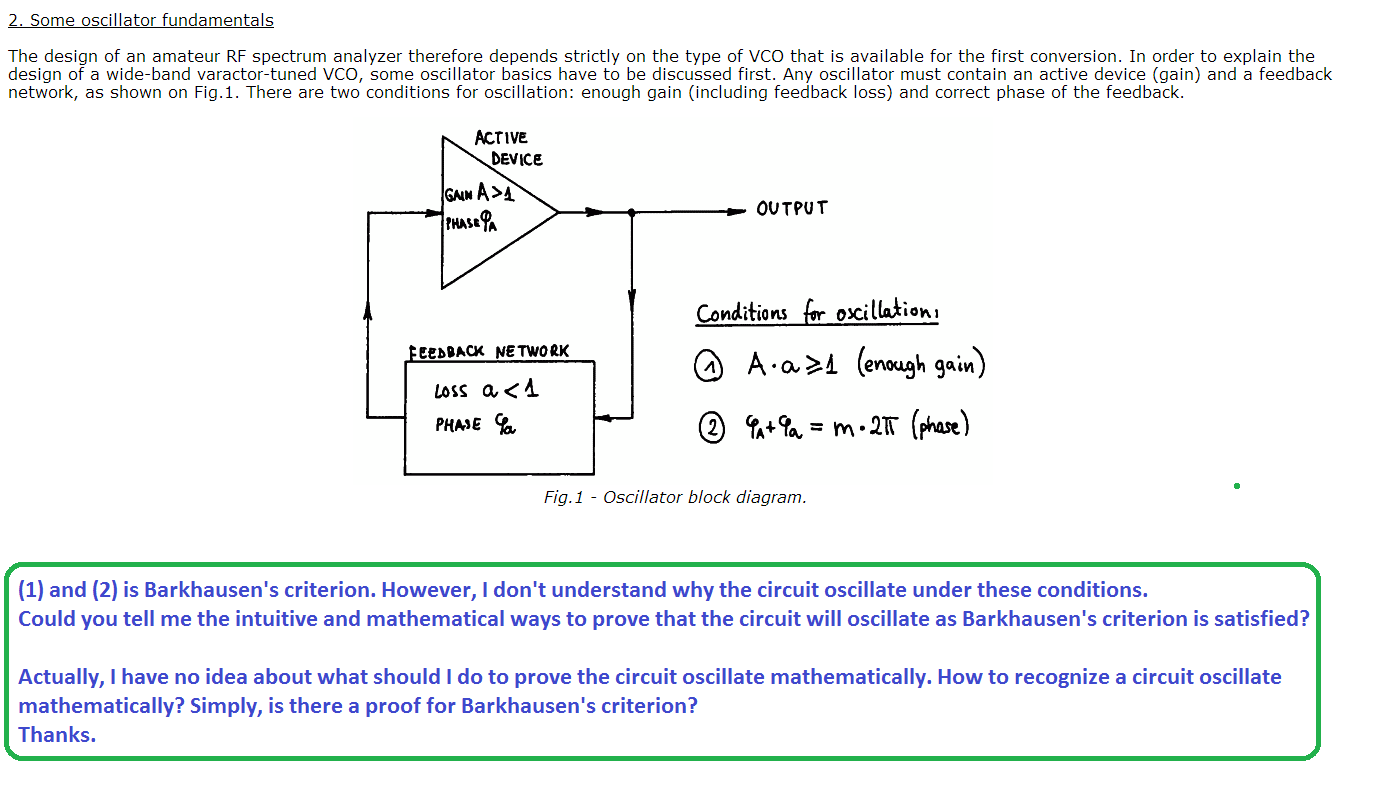
http://lea.hamradio.si/~s53mv/spectana/vco.html
Could you help me with the question in picture?

