MikeML,
Whoops, second mistake you made. You did not read my post #19 where I observe that if the product of R1,C1 and R2,C2 are equal, then the time constant terms cancel out. I should have spotted it first thing myself. So that circuit contains no exponential terms even though each of the caps have a time constant. You can see it in the formula for V1 reproduced again below.
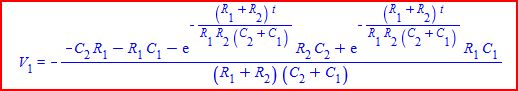
Ratch
Whoops, second mistake you made. You did not read my post #19 where I observe that if the product of R1,C1 and R2,C2 are equal, then the time constant terms cancel out. I should have spotted it first thing myself. So that circuit contains no exponential terms even though each of the caps have a time constant. You can see it in the formula for V1 reproduced again below.
Ratch
