Heidi
Member
Dear friends,
I was trying to derive the voltage of a capacitor from the current i(t)=I0*sin(2τft) through the capacitor, by using Q=CV.
Assume q(t) is the charge on one plate and the capacitor's initial voltage is zero. The following is what I did. Could you please tell me if there's anything wrong with the derivation for the cap voltage?
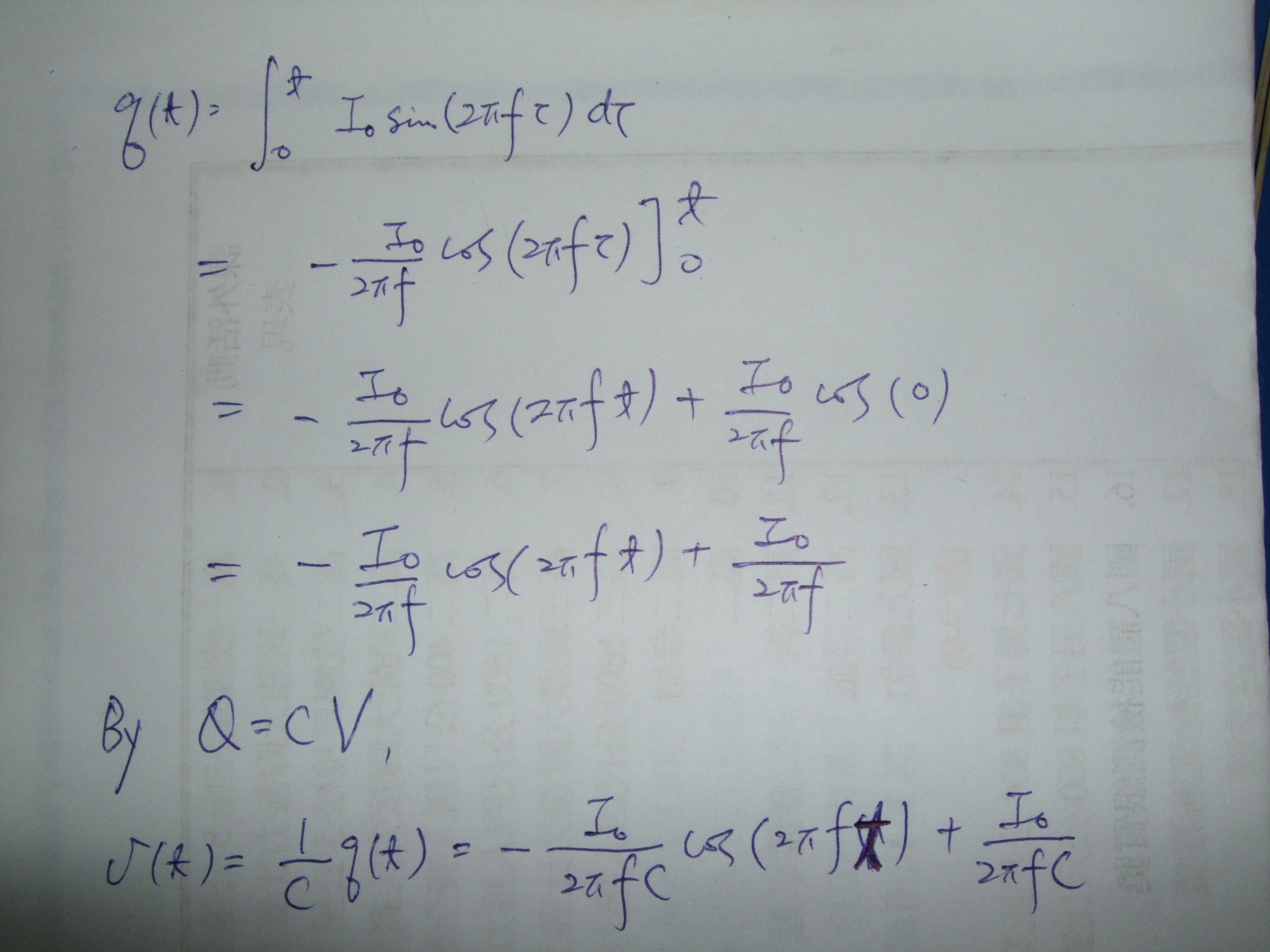
I was trying to derive the voltage of a capacitor from the current i(t)=I0*sin(2τft) through the capacitor, by using Q=CV.
Assume q(t) is the charge on one plate and the capacitor's initial voltage is zero. The following is what I did. Could you please tell me if there's anything wrong with the derivation for the cap voltage?
Attachments
Last edited: