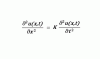calculus in electronics

[Ratchit]

A constant voltage source has zero source resistance. The capacitor will charge 'instantly' (the exponential function turns into a step response) in circuit theory. The problem with 'instantly' is that the universe doesn't work that way (division by zero issues).
View attachment 101062

The electric field inside the capacitor will not change 'instantly' (instead change as a Heaviside function) causing a delta-like displacement current, magnetic field and induced emf to counter the rise of current. (Lenz's law) So we will have finite charge time.

Correct, it will no change instantly. It will change in an infinitesimal amount of time. The current will approach infinity. Infinitesimal and infinity are limits, not definite values. In my example, the area under the current-time spike curve is 10 even when the resistance approaches zero.

Ratch

 

[Ratchit]

Hello again,

Well that's nice but you're allowing at least some resistance which is the only energy dissipator. If you show 99.9J and the cap only has 50J then you've got to show where that other 49.9 went, and it you want to say it is radiated then we have to see it being radiated in some form.

Not only that, but why do we say that there is only resistance and (possibly) only radiated power? There's also dielectric losses and inductance leading to a set of coupled PDE's such as:
Vx=-I*R-It*L
Ix=-V*G-Vt*C

where
I is the current,
V is the voltage,
Vx is the partial of V with x, x being a spatial variable,
Ix is the partial of I with x,
Vt is the partial of V with t, t being time,
It is the partial of I with t,
C is the capacitance per unit length assuming uniform cross section,
R is resistance per unit length,
G is equivalent dielectric conductance per unit length,
L is total series inductance per unit length.

And even that's an approximation because we'd have to handle the plate area and the leads differently.
We might also have to include another equation such as Vy=-Iy*R-Iyt*L for the plate in the other direction if we dont consider it uniform.
The main point is if we are to pick and choose what we want to allow, then we get off too easy and it turns out to be just a short cut.

But i guess i would settle for seeing the equation with the radiated energy being shown in one of the equations without assuming "it's just there somewhere".

I am only doing total resistance. I used 7 time constants in my integration. When I extend the limits to 15 time constants, then the value does show 100 joules to within machine precision. So there is some charge hiding under the tail of the graph.

Ratch

 

[nsaspook]

Hi,

I partially agree, but you're doing the same thing Ratch is doing now, which is picking and choosing what factors you want to include and which you dont. If you want to use the standard electric lumped circuit element, then we have something to talk about. If you want to include various things like fields then you might as well include lead resistance, because why include theory about the field and leave out something so simple as lead resistance and plate resistance. If you want to be realistic then be realistic, dont cut it short for no good reason.
The better equation would turn into a coupled PDE.

We are using an unrealistic example. So why waste time by not using perfect conductors if we can have infinite currents and infinitesimal times?

 

[The Electrician]

This is all old stuff:
https://www.physicsforums.com/threads/capacitor-charging-loss-not-the-two-capacitor-issue.292838/
https://www.hep.princeton.edu/~mcdonald/examples/twocaps.pdf
https://puhep1.princeton.edu/~mcdonald/examples/seriesrlc.pdf

And much more elsewhere.

 

[MrAl]

Hello again,

Well what i've seen so far is better than nothing i guess, and what i would have accepted several years ago without question, most likely, but today i see it differently.

For one for example, if we have two amplifiers and connect them together with an inductor (or capacitor) so the signal from the output of one feeds the input of the next stage, we have a certain circuit with a certain number of components. If we then short out that inductor, that action represents a change in topology. In a circuit connected with a resistor, that resistor dissipates energy and if we replace it with a short then there is no energy dissipated anymore, so zero energy.

There are problems that come up with zero resistance that dont come up even with 1 pOhm. But even if it was possible we always have Einstein to deal with. So far, nothing can go faster than the speed of light, and of course that includes energy.

The two PDE's i gave just for example decouple into two wave equations where the one for the voltage, and with all 'losses' set to zero we get a simple wave equation:
Vxx=K*Vtt (see attachment)

where Vxx is the second partial of V with x (spatial), and Vtt is the second partial of V with t (time).

The wave equation admits all sorts of solutions, but one of the interesting things is the velocity of the wave propagation can not exceed the speed of light. Since K is part inductance and appears as a factor, that means we cant have zero inductance. In fact, with a given capacitance we can not even have an inductance that is too low or else the equation will show a propagation velocity that is faster than the speed of light.

So again all we can do is try to accept that the examples are going to be a little fictitious, holding only in as much as their assumptions are called 'real'. That however means we have to have numerous examples to show what each set of assumptions leads to.

 

[MrAl]

Hello again,

I thought someone replied to this thread and that brought me back here and so i looked at part of it again.
What i realized was that there are a lot of ways of looking at this, but before i begin with that i must mention that i should have given Ratch more credit for doing that calculation independently which given what we had to work with was a good approach. Sometimes i get in my ultra realistic mood, mostly because i'm looking at something else privately (for example warped space and faster than light speed in such a space).
So "kudos" to Ratchit for the interesting calculation

One of the other approaches i was thinking about, which will again only consider certain things and not others, is to think about the current flow of electrons in the wires leading to the capacitor and how long it actually takes to transfer the known amount of charge to the capacitor. Since calculations like this have been done before, it should be relatively simple to calculate the time i takes for enough electrons to move into the capacitor until it gets charged up to 10.000000 volts. If anyone wants to try this here
We can still use zero ohms for the lead resistance i guess.
This is interesting i think because it will take a certain finite time for the cap to charge, which means no more zero time which contradicts all sorts of things and is just too unrealistic.

 

[nsaspook]

Interesting question.

**broken link removed**

For a perfect conductor (σ → ∞ ), the time constant goes to zero, meaning the charge density instantly dissipates.

 

[The Electrician]

Interesting question.

**broken link removed**

So is this the "relaxation time" of a non-uniform charge distribution?

Here: https://encyclopedia2.thefreedictionary.com/Relaxation+time+of+electrons

the very last sentence says, for a superconductor (which is a perfector conductor?): "The relaxation time thus becomes infinite (as nearly as can be measured), a rare macroscopic manifestation of a quantum effect."

 

[MrAl]

Hi,

Not sure what part of the paper you were referring to about the 'relaxation time" but it looks like it might be viewed as simple inertia, although i dont know if the numbers work out like simple inertia would given the tiny masses. So it sounds like an object moving in free space, if it doesnt hit anything it never stops. Apparently they are only talking about low temperature superconductivity too where the electrons travel in pairs.

I did a rough calculation of the charging cap using the idea that the electrons travel at a certain rate near room temperature but the resistance is allowed to be either zero or very very small, and no other allowed influences. The information for the speed can be found on Wikipedia.
It led to a time of about 5.4ns for a very thin wire of length 1 meter which i assume is also the return path length. Interesting though was that the overall speed comes out to close to 66.7 percent of the speed of light, which matches many transmission line speeds. Not so interesting was the 'equivalent' resistance would have to have been way down near 1e-10 ohms which is not realistic at all, but then we can call that zero if we attribute the delay to the natural inductance and capacitance i guess which limits everything.

Interesting reads.

Also we cant forget about Agent Skinner
The skin effect would be strong near the start of any fast rising wavefront.