angular motion

[JimB]

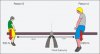
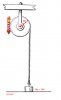
You are correct that a larger disc made from similar material will have a larger moment of inertia (when I studied this stuff 20 odd years ago, we used a different expression for "moment of inertia", but I cannot remember right now what is was.).

The moment if inertia will only have an effect when there is angular acceleration (RPM changes), if I understand the current question, it is to do with a pulley pulling on a rope at a constant speed, no acceleration involved.

The "simplification" I was referring to was the various forces on the pulley/crankshaft.
As well as the torque component, the force due to the rope also creates a downward force on the pulley/shaft mounting.
This is probably not directly relevant in this example, but for a full analysis of the forces using a "free body diagram" it is essential.

JimB

 

[Tony Stewart]

Kids learn how to swing higher by increasing their angular momentum by adding kinetic energy at the right time swinging their legs back and forth.


more....

In addition, the fast learners learn to accelerate the swing more by bending the direction of centripetal force by pushing and pulling the chain or rope towards the vertical center which creates a tangential vector of force at right angles to the the radial vector of inertia. This accelerates the rise in momentum of oscillating inertia when the swing velocity is too low for the leg movement to have much effect. This static bidirectional force near the middle of the hanging swing has more torque effect than the kinetic motion of the feet. However both inputs result in the greatest inertia. Also no external pushes are needed by grandpa if these horizontal push-pull vectors are applied towards the center. This is the physics of swinging by static tangential forces of the arms then later the boost with kinetic energy added in the direction of angular momentum.

The change of Moment of Inertia is relatively small compared to the spinning skater. It is possible to demonstrate with relatively little kinetic energy that one can alternate between high and low speeds with small and large centripetal radius without much change in the two speeds, thus making the kinetic energy a relatively small factor. This can be demonstrated on the playground with the rotating platform by swing the leg in and out to change rotational speeds back and forth.

 

[PG1995]

Thank you, JimB, Tony Stewart.

Torque is going to be zero when angular acceleration is zero. Thing of linear motion where F=ma which means that if acceleration is zero then the force has to be zero.

A net force on any mass results in acceleration. Even a tiny bit of force can accelerate a mass no matter how small assuming there is no friction involved.

Q1:
This question is about the interpretation of angular torque.

Please have a look here.

The radius of pulley is 1m and it can rotate freely without any friction. The rocket is firmly connected to the edge of pulley so that the pulley and rocket rotate together.

Suppose that the moment of inertia of pulley is 20 kg.m^2. Let's ignore the mass of rocket itself. Don't forget that moment of inertia is equivalent to mass in angular motion.

T=Fr=20(1)=20 Nm.
T=Iα=20(α)
=> α=20/20=1 rad/sec.

The pulley will accelerate at a rate of 1 rad/sec. Do you agree?

Q2:
Please have a look here.

The rocket is firmly connected to the edge of pulley so that the pulley and rocket rotate together. The radius of pulley is 1 meter and the weight to be lifted is 20 N.

The clockwise torque due to the suspended weight is 20 Nm and the counterclockwise torque is 30 Nm. That leaves us with net counterclockwise torque of 10 Nm.

The pulley's moment of inertia is 20 kg.m^2.

T=Iα
=> α=10/20=0.5 rad/sec.

It means that the pulley is going to accelerate at the rate of 0.5 rad/sec. Personally, I don't think that it's correct because 2 kg mass is also suspended so when the pulley accelerates the mass will also accelerate, and it means we also have to account for 2 kg mass too. Thank you.

Regards
PG

 

[Tony Stewart]

As I recall from my swinging days, pushing and pulling the chain away at right angles to the gravitational force and leaning in the opposite direction causes a tangential force towards the new pivot point. THis works even when not moving your feet AND starting from a static position by creating an offset to the centre pivot point. It works throughout the full growth of the oscillating cycle up to +/-45 deg but to get to +/- 90deg requires both static forces on the chain and swinging moments with the feet and shifting center of mass.

 

[steveB]

PG,

Your answers are correct above, but for one mistake. Watch your units. Angular acceleration has units of rad/s/s, not rad/s.

 

[Tony Stewart]

I dont know if these were PG's answers or an illustration he copied.
The intent was to compare a weightless Pulley with Mass of 10kg to a flywheel pulley with same moment of inertia and notation of acceleration was also incorrect..

 

[steveB]

I dont know if these were PG's answers or an illustration he copied.
The intent was to compare a weightless Pulley with Mass of 10kg to a flywheel pulley with same moment of inertia and notation of acceleration was also incorrect..

I interpreted his question to be a copy of illustrations from a text and then the yellow highlighted part is his answers to the questions posed.

Can you explain in what way the notation for acceleration is incorrect?

 

[Tony Stewart]

The geometry and mass distribution will affect the angular momentum and rotational acceleration only according to the conservation of energy since the angular momentum is increasing while the potential energy is decreasing.

Nothing has been stated about these parameters which affect angular acceleration.

 

[steveB]

The geometry and mass distribution will affect the angular momentum and rotational acceleration only according to the conservation of energy since the angular momentum is increasing while the potential energy is decreasing.

Nothing has been stated about these parameters which affect angular acceleration.

I can't say I'm following what your point is. What you say above is correct. Geometry and mass distribution do affect angular momentum and rotational acceleration, but this "affect" is captured by the rotational inertia, which is specified. Energy conservation always holds, but we can analyze the situation using torques/forces and ignore the energy. The rocket is using chemical energy to provide the force, and the mass on the rope is using gravitational energy to provide the force. The specification of the forces from the rocket and the weight on the rope is enough to solve the problem.

Hence, I disagree with your statement that "nothing has been stated about these parameters which affect angular acceleration". The forces, and nature of the objects tells us all we need to know to solve the specific question, at least under the highly idealized assumptions stated.

 

[PG1995]

Thank you, Tony Stewart, Steve.

Your answers are correct above, but for one mistake. Watch your units. Angular acceleration has units of rad/s/s, not rad/s.

Sorry about the units for angular acceleration.

I believe that you agree with what I'm in saying in Q1 in my previous post.

This is what I said at the end of Q2:
"It means that the pulley is going to accelerate at the rate of 0.5 rad/sec/sec. Personally, I don't think that it's correct because 2 kg mass is also suspended so when the pulley accelerates the mass will also accelerate, and it means we also have to account for 2 kg mass too."

Basically I was trying to say that the pulley will not accelerate at the rate of 0.5 rad/sec/sec but I don't know how to incorporate the effect of 2 kg mass into the calculation. In other words, what would be the (angular) acceleration for pulley and the suspended mass for the case shown in Q2?



Archimedes once reportedly said, "Give me a place to stand on and I can lift the earth". I understand that he didn't really mean it in literal terms but rather he was just trying to make a point. For more information, you can have a **broken link removed**.

One can lift a heavy stone with relatively less effort using a long lever according to the torque principle as shown here. Why does a long lever makes the job easier? What's the reason behind this? Thank you.

Regards
PG

Helpful links:
1: https://physics.stackexchange.com/questions/67892/origins-of-moment-of-inertia (this explains why moment of inertia is mr^2 and not something else etc.)
2: https://answers.yahoo.com/question/index?qid=20141121023557AAb3iQ2 (this tries to touch the question of why moment of inertia is called so.)

 

[steveB]

PG,

You are correct about the mass of the weight on the rope will add inertia to the system and should be included in a more precise calculation. I interpreted the analysis to be highly idealized. The mass of the rocket was ignored and so I would also ignore the mass of the rope and weight. But of course you could add those into the calculation. I guess the thing to realize is that an inertia of 20 kg m^2 is quite large and the mass of 2 kg is not the major source of inertia.

If you do want to include the mass, then simply realize that F=ma is an added force putting tension on the rope. Approximately, you can estimate the order of magnitude of the added force by considering your answer of 0.5 rad/s/s. This acceleration translates to a linear acceleration of 0.5 m/s/s and since the mass is 2 kg, then the force is 1 N, which changes the torque by 1 Nm. As I mentioned this is relatively small compared to the 10 Nm net torque, but you could include the effect if you choose. I leave it to you to modify the analysis to include the force from the accelerating mass.

 

[steveB]

Why does a long lever makes the job easier? What's the reason behind this? Thank you.

The lever changes the distance and force required to lift an object, but keeps the work (or energy) required the same. Work is the integral of force over distance, or simple force times distance in simple situations. So when you use a lever, the Work=Force x Distance is the same, but you generally use the lever to reduce the force and increase the distance to do your work.

Why does this make it easier? Simply because humans and machines have limited force that they can apply, but if the total work is within the capability of the machine doing the work, then the lever brings the required force into the range of capability of the machine.

By the way, Archimedes can't lift the earth, not only because the lever will break and he has no where to stand, but also because a human does not have the stored energy to do that much work.

 

[Tony Stewart]

Unless you can define the inertial mass of the pulley it is the not the same as a massless pulley with a linear circumferential force.

One has to know both the inertial mass of pulley and torque of external suspended mass by its product in the same nits of measure to know the change if rotational energy, linear energy and potential energy by conservation of energy as angular moment is not conserved. It increases with loss of m*g*h according the differences.

For this reason a sphere rolls always faster than any hollow cylinder of same diameter down the same incline. Due to smaller moment of inertia. Likewise for a pulley and mass.

 

[steveB]

Tony Stewart,

I'm still not able to connect the dots of what you are saying. I don't find myself disagreeing too much with your words. But I'm not able to see the relevance of those words to PGs problem.

Maybe I'm just missing the point, so there is no need for me to figure it out as long as PG either understands you or if he has resolved his question.

 

[PG1995]

Thank you, Steve.

Tony Stewart: I'm also not able to understand what you are saying. I didn't say that the pulley is massless. I believe that you misread something in the orginal post on the current discussion.

You are correct about the mass of the weight on the rope will add inertia to the system and should be included in a more precise calculation. I interpreted the analysis to be highly idealized. The mass of the rocket was ignored and so I would also ignore the mass of the rope and weight. But of course you could add those into the calculation. I guess the thing to realize is that an inertia of 20 kg m^2 is quite large and the mass of 2 kg is not the major source of inertia.

I understand that but I still don't really find the comparison justified. Although moment of inertia is considered to be an equivalent of mass in angular motion, we still cannot add moment of inertia to mass. "20 kg m^2" means a point mass of 20 kg rotating at a distance of 1 m from rotation axis and well "2 kg" mass is just 'typical' mass!

If you do want to include the mass, then simply realize that F=ma is an added force putting tension on the rope. Approximately, you can estimate the order of magnitude of the added force by considering your answer of 0.5 rad/s/s. This acceleration translates to a linear acceleration of 0.5 m/s/s and since the mass is 2 kg, then the force is 1 N, which changes the torque by 1 Nm. As I mentioned this is relatively small compared to the 10 Nm net torque, but you could include the effect if you choose. I leave it to you to modify the analysis to include the force from the accelerating mass.

In my humble opinion, the angular acceleration for pulley due to counterclockwise torque of 10 Nm cannot be 0.5 rad/s/s because this value was calculated just considering the moment of inertia of pulley. I believe that we need to find the effect of torque on both pulley and mass simultaneously then the angular acceleration of pulley will exactly translate into linear acceleration of the mass.

But still let's do it the way you are suggesting. You are saying that the value for angular acceleration which I calculated to be 0.5 rad/s/s gets translated to 0.5 m/s/s. According to F=ma for linear motion, F=1 N. You said that this force changes the torque by 1 Nm although I don't exactly understand what it really means. Probably you are saying that this 1 Nm clockwise torque gets subtracted from 10 Nm counterclockwise torque and therefore the net torque is 9 Nm counterclockwise. If this is really what you were suggesting then the fallacy in our calculation is quite apparent.

The lever changes the distance and force required to lift an object, but keeps the work (or energy) required the same. Work is the integral of force over distance, or simple force times distance in simple situations. So when you use a lever, the Work=Force x Distance is the same, but you generally use the lever to reduce the force and increase the distance to do your work.

Why does this make it easier? Simply because humans and machines have limited force that they can apply, but if the total work is within the capability of the machine doing the work, then the lever brings the required force into the range of capability of the machine.

By the way, Archimedes can't lift the earth, not only because the lever will break and he has no where to stand, but also because a human does not have the stored energy to do that much work.

In general, I do agree with you that the energy required remains the same. In torque force and distance are right angle to each other and therefore the work done is zerowhich means you are talking about the other distance which is in direction of the force. Please have a look here. Suppose that in the seesaw picture, the person weighing 1000 N is already sitting on one side of the seesaw and the given side is touching the ground. The other guy who just weighs 500 N can balance the seesaw and raise the heavy guy from the ground to same height as his. How and why? Thank you.

Regards
PG

 

[JimB]

Suppose that in the seesaw picture, the person weighing 1000 N is already sitting on one side of the seesaw and the given side is touching the ground. The other guy who just weighs 500 N can balance the seesaw and raise the heavy guy from the ground to same height as his. How and why?

Take moments about the pivot point.
Consider clockwise moment to be +ve
For the beam to be in equilibrium, the sum of moments must be zero.

Moments for the big guy (Mbg) = L x M = +1 x 1000 = +1000 Nm (Clockwise)

Moments for the little guy (Mlg) = L x M = -2 x 500 = -1000 Nm (Anti-Clockwise)

Net Moment = Mbg + Mlg = 1000 + (-1000) = 0

OK?

JimB

 

[steveB]

I understand that but I still don't really find the comparison justified. Although moment of inertia is considered to be an equivalent of mass in angular motion, we still cannot add moment of inertia to mass. "20 kg m^2" means a point mass of 20 kg rotating at a distance of 1 m from rotation axis and well "2 kg" mass is just 'typical' mass!

In my humble opinion, the angular acceleration for pulley due to counterclockwise torque of 10 Nm cannot be 0.5 rad/s/s because this value was calculated just considering the moment of inertia of pulley. I believe that we need to find the effect of torque on both pulley and mass simultaneously then the angular acceleration of pulley will exactly translate into linear acceleration of the mass.

But still let's do it the way you are suggesting. You are saying that the value for angular acceleration which I calculated to be 0.5 rad/s/s gets translated to 0.5 m/s/s. According to F=ma for linear motion, F=1 N. You said that this force changes the torque by 1 Nm although I don't exactly understand what it really means. Probably you are saying that this 1 Nm clockwise torque gets subtracted from 10 Nm counterclockwise torque and therefore the net torque is 9 Nm counterclockwise. If this is really what you were suggesting then the fallacy in our calculation is quite apparent.

PG, you are misreading what I actually said. Please go back and reread what I wrote about these things very carefully. Also, I'll try to clarify a little bit about what you are misreading.

First, I did not say say you can add mass to moment of inertia. In fact there is a way that you can add an equivalent moment of inertia from the mass, but this would be a mathematical equivalence, analogous to making an equivalent circuit. However, I deliberately did not suggest this, since I thought it would be confusing for you at this stage of learning this subject.

Your second paragraph above is correct, and this is exactly what I was agreeing with you about in my response. So I can repeat that I agree with your opinion.

You misrepresented "the way I suggested". I was not suggesting that that was the way to precisely calculate the answer. I clearly stated "approximately, and to get the order of magnitude". I was just making some estimation of the effect to see if it is significant. Since the estimate came out to be of the order of 10% modification to your initial answer, I think we can conclude that it is reasonable to try and include the effect of the mass, just as your intuition told you we should do. If the estimate had revealed that the modification was 10 orders of magnitude below the major effects, then we would decide to ignore the effect of the mass.

I actually did not tell you exactly how to do the calculation, but said "i leave it to you ...". There are ways to write the equations to get all constraints to be met, and there is more than one way to do it, I would expect.

 

[steveB]

Suppose that in the seesaw picture, the person weighing 1000 N is already sitting on one side of the seesaw and the given side is touching the ground. The other guy who just weighs 500 N can balance the seesaw and raise the heavy guy from the ground to same height as his. How and why? Thank you.

Ok, JimB answered this in a way appropriate for engineers and scientists. We develop an understanding of nature, and create a mathematical model of the approximate way we expect experiments to behave. Here, approximate means within experimental accuracy. In this case we have Newton's laws to help us analyze the situation using various idealizations of the real situation. Using our mathematical model, which we now understand very well, we can do calculations to demonstrate how the smaller guy can balance the bigger guy.

As to why this is true, that is a harder question from a scientific point of view. Ultimately, we never get to the final "why" in physics, but we can always try to probe deeper. In this case, we could consider that the see-saw is not really an ideal rigid object. It is composed of atoms. There are atomic forces (electrical in nature) that keep the board together as one piece and provides forces and torques within the system. We could try to analyze every atom and do a free body diagram for each and every one, but this is of course impossible for a person to do and would take a computer an impractical amount of time to complete. But, in principle we could try to imagine how all these electrostatic forces are interacting to create a nearly rigid board that transmits forces and torques to the people involved in having fun on a see-saw.

 

[steveB]

PG,

I thought I would write out two approaches to solving the pulley/rocket/mass problem.

Method 1: Straightforward Force/Torque Analysis

Let the rocket force be represented by Ft=30N and the tension in the rope by Fr, which we will need to calculate. The pulley inertia is I=20 kg m^2 and the mass is m=2 kg, suspended in a gravitational field with g=10 m/s/s.

The torque equation becomes α=dω/dt = (R Ft - R Fr) / I , which leaves only the rope tension as an unknown to be calculated/represented.

The rope tension is caused by the force from the mass, and the mass has two components of force that cause rope tension, gravitational force (mg), and inertial force m dv/dt. Hence, Fr=m g+m dv/dt, where v is the linear velocity of the mass.

However, linear velocity of the mass v can be related to the rotational acceleration of the pulley by v=R ω, and since R does not change in time then dv/dt = R dw/dt=Rα.

We can now substitute this into the original torque equations and do some algebra to find that α=( R Ft - R m g )/ ( I + m R^2)

In our case we get α = ( (1) 30 - (1) 2 (10) ) / ( 20 + 2 (1)^2 )=10/22=0.4545 rad/s/s

This answer is lower than the 0.5 rad/s/s , as you predicted.

Method 2: Equivalent Inertia Transformation

With experience, we can develop many tricks. We do tricks all the time in circuit theory by creating equivalent circuits that are physically different representations of the same mathematical problem.

In this case, you can observe that the effect of the 2 kg mass inertia is to add an effective rotational inertia to the pulley. This allows us to use your original simple method, but we modify the calculation to use equivalent inertia Ie rather than actual inertia I. The equivalent inertia acts as if the pulley had the total mass of 2 kg stuck to it at the outer radius where the rope applies the force (1 meter in this case), hence Ie=I+mR^2=20+2(1)^2=22 kg m^2.

We now treat the problem in a simple way and we can say that torque is T= Ie α, hence α=T/Ie=FR/Ie, where F is the sum of the tangential forces trying to turn the pulley. The rocket gives force Ft and the gravitational force gives -mg and we get α = R ( Ft-mg )/(I+mR^2), and this is the same as the answer giving by method 1.

I would discourage you from using Method 2 until you are comfortable with Method 1. In a sense, Method 1 is the proof that Method 2 is allowed, but once you know it, you can use method 2 in similar situations and save some time. You always need to be careful with equivalent methods to make sure that you are not violating any assumptions implicit in the derivation of the equivalent method. For this reason, whenever I use an equivalent method in real important work, I double check it with the rigorous approach. Hence, these shortcuts increase my work-load rather than reduce it. But, it is often nice to have a simple method (fully verified) that you can present to other people so that they can understand without doing a lot of work.

 

[PG1995]

Thank you, JimB, Steve.

Steve, you still remember a lot of physics!

Method 1: Straightforward Force/Torque Analysis

Let the rocket force be represented by Ft=30N and the tension in the rope by Fr, which we will need to calculate. The pulley inertia is I=20 kg m^2 and the mass is m=2 kg, suspended in a gravitational field with g=10 m/s/s.

The torque equation becomes α=dω/dt = (R Ft - R Fr) / I , which leaves only the rope tension as an unknown to be calculated/represented.

The rope tension is caused by the force from the mass, and the mass has two components of force that cause rope tension, gravitational force (mg), and inertial force m dv/dt. Hence, Fr=m g+m dv/dt, where v is the linear velocity of the mass.

However, linear velocity of the mass v can be related to the rotational acceleration of the pulley by v=R ω, and since R does not change in time then dv/dt = R dw/dt=Rα.

We can now substitute this into the original torque equations and do some algebra to find that α=( R Ft - R m g )/ ( I + m R^2)

In our case we get α = ( (1) 30 - (1) 2 (10) ) / ( 20 + 2 (1)^2 )=10/22=0.4545 rad/s/s

This answer is lower than the 0.5 rad/s/s , as you predicted.

I would go with the first method because it seems more natural and straightforward.

Let's do another case. This time the pulley is already rotating with angular velocity, ω, of 2π rad/s. There is no angular acceleration which means torque is zero and if we further assume that there is no friction involved then the rocket isn't really doing any work; it's basically in off mode.

The setup looks like this. But this time as I mentioned above the pulley was already rotating at a constant angular velocity of 2π rad/s which translates to linear velocity of 2π m/s when the rope which has 2 kg mass suspended to it and resting on ground gets somehow attached to it. The vertical height between the pulley and ground could be approximated to be 20 meters.

Our purpose is to lift the mass to some height above the ground and we also want to keep things as calm as they could be; I mean no jerky motion.

We can assume that the rocket has some kind of a sensor which regulates the angular velocity at 2π rad/s. It turns the rocket on if the velocity is under 2π rad/s and off if it goes above. Further, we can also assume that the sensor makes rocket to exert different amount of force as required.

As soon as the rope gets attached to the pulley, the angular velocity of pulley will go down for an infinitesimal amount of time and during that time both pulley and mass would have same speed.

Then, instantly, the rocket turns on and starts exerting force. The rocket aims to get the system to 2π rad/s within 1 second. Therefore the system needs the acceleration of (2π-5. 9924)/1s=0.291 rad/s/s for one second. This time we need to know rocket force and I believe that the formula derived by you can be used, α=( R Ft - R m g )/ ( I + m R^2). After rearranging Ft={α/(R(I+mR^2))}+mg={0.291/(20+2)}+2(10)=20.013 N. Once the system has reached 2π rad/s angular velocity then the rocket just has to exert 20 N force to counterbalance the clockwise torque to 2 kg mass. Do you agree with everything I have said?

As to why this is true, that is a harder question from a scientific point of view. Ultimately, we never get to the final "why" in physics, but we can always try to probe deeper. In this case, we could consider that the see-saw is not really an ideal rigid object. It is composed of atoms. There are atomic forces (electrical in nature) that keep the board together as one piece and provides forces and torques within the system. We could try to analyze every atom and do a free body diagram for each and every one, but this is of course impossible for a person to do and would take a computer an impractical amount of time to complete. But, in principle we could try to imagine how all these electrostatic forces are interacting to create a nearly rigid board that transmits forces and torques to the people involved in having fun on a see-saw.

I would say that JimB's reply was regular and typical answer to the question. I was more interested in 'why'. I'm happy that you understood my query and I do agree that such a simple question might be really hard to answer. It's like asking that why the inertia exist in the first place.



This question came to my mind while writing about the case when the pulley rotating at constant angular velocity gets connected to the rope. The pulley possessed angular moment and momentum is always conserved; linear and angular momentums work independent of each. When the pulley gets joined/connected to rope and mass starts get lifted, some of angular momentum gets transformed into linear momentum. I don't see how angular momentum is conserved in this case.

Let's try a simple case. Suppose a bicycle is being driven at a constant speed which means constant angular velocity and hence angular momentum. Once the brakes are applied, where does angular momentum disappear? Thank you.

Best regards
PG

Some good links about linear and angular momentums:
1: https://ccrma.stanford.edu/~jos/pasp/Relation_Angular_Linear_Momentum.html
2: https://www.physicsforums.com/threa...nation-of-angular-and-linear-momentum.473302/
3: https://imechanica.org/node/8288