Mr RB
Well-Known Member
Hi, I'm making a "precision" 1kHz sine wave generator, using a PIC 16F628 and 20MHz xtal.
Goals;
1. Sine freq 1000Hz high freq accuracy, xtal locked
2. Sine amplitude "exactly" 2v p/p set by 5v regulator and trimpot good enough
3. Sine distortion as low as possible using simple external filter parts
4. Low-ish output impedance to connect to audio amp inputs etc
5. Minimum parts as it is an open source project for everyone
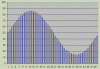
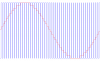
The xtal has been trimmed to 20Mhz better than 1PPM, and the 1kHz sine is generated by PIC PWM with 50 entries in a jitter-free sine table at exactly 20uS per entry. The sine table I made in Excel is shown below.
The PWM has a resolution of 100 steps, and sine table runs an amplitude of 73 PWM steps from PWM of 14 to PWM of 86. It is equally distributed +/- from PWM 50 so there is no distortion and each sine sample has been rounded the correct direction so amplitude error in any sine PWM sample is less than about 0.68% of the total amplitude.
The idea is that since the PIC and mathematical sine tabe already produces excellent frequency and good basic sine shape (ie the hard stuff ie done), so that addition of a simple passive filter will be all that is needed.
The PIC sine part is working perfectly and it generates a sine from the 50 samples with an exact freq of 1kHz (around 1000.0000 Hz +/- 0.0005Hz).
The PIC hardware is simplicity itself at this point, just the 0v-5v PWM coming out the PIC pin, and I tacked a trimpot and 0.22uF cap RC filter on that for testing.
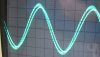
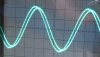
The trimpot was adjusted to take out the bulk of the hash without reducing the amplitude or changing the shape of the sine. RC filter as seen in the photos below; 482 ohms, 0.221uF, sine amplitude 3v p/p.
Now the question!
I have lots of parts avaliable including toroid formers and quality caps of different types, cap and inductance meters etc, and a 'scope, but no proper distortion measuring equipment. What would be the best simple passive filter to attach to this PWM output to give the desired "low distortion" result at 1kHz 2v p/p?
My filter design knowlege is poor, limited to googling "Chebychase filter calculator" on some rare occasions... (grin)
Goals;
1. Sine freq 1000Hz high freq accuracy, xtal locked
2. Sine amplitude "exactly" 2v p/p set by 5v regulator and trimpot good enough
3. Sine distortion as low as possible using simple external filter parts
4. Low-ish output impedance to connect to audio amp inputs etc
5. Minimum parts as it is an open source project for everyone
The xtal has been trimmed to 20Mhz better than 1PPM, and the 1kHz sine is generated by PIC PWM with 50 entries in a jitter-free sine table at exactly 20uS per entry. The sine table I made in Excel is shown below.
The PWM has a resolution of 100 steps, and sine table runs an amplitude of 73 PWM steps from PWM of 14 to PWM of 86. It is equally distributed +/- from PWM 50 so there is no distortion and each sine sample has been rounded the correct direction so amplitude error in any sine PWM sample is less than about 0.68% of the total amplitude.
The idea is that since the PIC and mathematical sine tabe already produces excellent frequency and good basic sine shape (ie the hard stuff ie done), so that addition of a simple passive filter will be all that is needed.
The PIC sine part is working perfectly and it generates a sine from the 50 samples with an exact freq of 1kHz (around 1000.0000 Hz +/- 0.0005Hz).
The PIC hardware is simplicity itself at this point, just the 0v-5v PWM coming out the PIC pin, and I tacked a trimpot and 0.22uF cap RC filter on that for testing.
The trimpot was adjusted to take out the bulk of the hash without reducing the amplitude or changing the shape of the sine. RC filter as seen in the photos below; 482 ohms, 0.221uF, sine amplitude 3v p/p.
Now the question!
I have lots of parts avaliable including toroid formers and quality caps of different types, cap and inductance meters etc, and a 'scope, but no proper distortion measuring equipment. What would be the best simple passive filter to attach to this PWM output to give the desired "low distortion" result at 1kHz 2v p/p?
My filter design knowlege is poor, limited to googling "Chebychase filter calculator" on some rare occasions... (grin)
Attachments
Last edited: