AtomSoft
Well-Known Member
need some help 
i got a LM75(BD) and can only get so far.. its I2C and so far i can read from it i think heh
Im using the below code to split the 2 byte data (temperature) into 1 byte then into 3 bytes...
and code to get info:
My entire code is quite long. Not sure if i should post it heh... the I2C is in my PDF cheat sheet and worked before so i assume its not the code for that or the hardware since i get a int like 0x02FF and such...
I assume it the way i convert the stuff or something or read the bytes in..
EDIT:
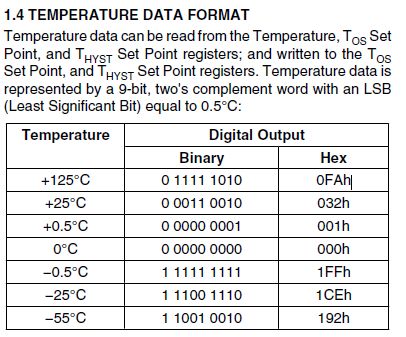
Here is some valuable info which i dont understand much:
"
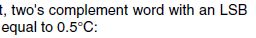 "
"
i got a LM75(BD) and can only get so far.. its I2C and so far i can read from it i think heh
Im using the below code to split the 2 byte data (temperature) into 1 byte then into 3 bytes...
Code:
temp3 = ReadLM75BD(); //get 2 bytes (int)
temp4 = temp3 >> 8; // erase the LSByte (the LSBit is not important i assume)
tH = (temp4 / 100) + 0x30; // divide by 100 to get hundreds #
tT = ((temp4 % 100) / 10) + 0x30; // divide by 100 and use remainder to divide by 10 to get tens #
tO = (((temp4 % 100) % 10) % 10) + 0x30; //use remainder on of temp4/100 then divide that byt 10 and with that remainder divide it by ten and use last remainder as ones...and code to get info:
Code:
unsigned int ReadLM75BD(void){
unsigned int tmp;
char result;
i2c_start(); //Send Start
i2c_write(RAdd); //Send our Device Address with the Write BIT
result = i2c_ack2(); //Test for ACK
tmp = i2c_read(); //Read 1 Byte from device and save in tmp
result = i2c_ack2(); //Test for ACK
tmp = tmp << 8;
tmp |= i2c_read(); //Read 1 Byte from device and save in tmp
result = i2c_ack(); //Test for NACK
i2c_stop(); //Send Stop
return tmp;
}My entire code is quite long. Not sure if i should post it heh... the I2C is in my PDF cheat sheet and worked before so i assume its not the code for that or the hardware since i get a int like 0x02FF and such...
I assume it the way i convert the stuff or something or read the bytes in..
EDIT:
Here is some valuable info which i dont understand much:
"
Last edited:

