Equation of Vc

[Archit]

I am trying to solve the following sub-circuit but having a hard time in finding equation of Vc(t).I I will be highly obliged if someone could solve it for me.
Initial conditions:
iL(0)=ILmax
ip(0)=Ip0
Vc(0)=Vc0
Final Condition:
ic(t_final)=0;
i.e. this subinterval will stop when ic=0
or iL(t) becomes equal to ip(t)
Note:Vp=0
Edit 1: One can assume iL is constant as Lin is a large value

Thanking in anticipation

 

[alec_t]

Welcome to ETO!
Is this a school/college assignment?

 

[Archit]

Not assignment, It is the sub-circuit of a topology for smps for my project.

 

[Archit]

Welcome to ETO!
Is this a school/college assignment?

Not assignment, It is the sub-circuit of a topology for smps for my project.

 

[Archit]

Please. can anyone help

 

[dknguyen]

I am trying to solve the following sub-circuit but having a hard time in finding equation of Vc(t).I I will be highly obliged if someone could solve it for me.
Initial conditions:
iL(0)=ILmax
ip(0)=Ip0
Vc(0)=Vc0
Final Condition:
ic(t_final)=0;
i.e. this subinterval will stop when ic=0
or iL(t) becomes equal to ip(t)
Note:Vp=0
View attachment 113942
Thanking in anticipation

Transient analysis is a PITA. Especially by hand. That's all I really have to say. I'd find an online simulator and punch that into it. Otherwise you're dealing with solving differential equations after doing a mesh analysis. I don't think that would be quite far enough to get you where you want to either since you're interested in a unsteady state transient condition.

It looks like this, except yours is more complicated than any of the circuits shown:

So yeah...simulate that. Cuz that be nasty and I'm not really sure you'd get anything meaningful out of the result anyways.

 

[crutschow]

If this is not homework then simulation is definitely the way to go.
Have you used Spice simulators before?

 

[Archit]

If this is not homework then simulation is definitely the way to go.
Have you used Spice simulators before?

Yeah I have used but I want the equations and dependance of Vc(t) on the Ip, and iL. It will further help me to choose the values of Rc and Cc.

 

[Archit]

Transient analysis is a PITA. Especially by hand

Agreed.

 

[Archit]

Transient analysis is a PITA. Especially by hand. That's all I really have to say. I'd find an online simulator and punch that into it. Otherwise you're dealing with solving differential equations after doing a mesh analysis. I don't think that would be quite far enough to get you where you want to either since you're interested in a unsteady state transient condition.

It looks like this, except yours is more complicated than any of the circuits shown:

So yeah...simulate that. Cuz that be nasty and I'm not really sure you'd get anything meaningful out of the result anyways.

Please see, the problem once again as I have editted my problem. Thankyou

 

[MrAl]

I am trying to solve the following sub-circuit but having a hard time in finding equation of Vc(t).I I will be highly obliged if someone could solve it for me.
Initial conditions:
iL(0)=ILmax
ip(0)=Ip0
Vc(0)=Vc0
Final Condition:
ic(t_final)=0;
i.e. this subinterval will stop when ic=0
or iL(t) becomes equal to ip(t)
Note:Vp=0
Edit 1: One can assume iL is constant as Lin is a large value
View attachment 113942
Thanking in anticipation

Hello,

If you are treating iL as a constant current, then the response is probably just 2nd order which is fairly simple in the world of mathematical circuit analysis.

So let me get thjis right now:
1. iL is considered constant for the entire time you want to do the analysis for?
2. The input Vin, is that a battery or just DC supply?
3. The little input cap is not significant?

 

[Archit]

1. iL is considered constant for the entire time you want to do the analysis for?

Yes it is constant.

2. The input Vin, is that a battery or just DC supply?

DC supply

3. The little input cap is not significant?

Yes it is insignificant.

 

[MrAl]

Yes it is constant.

DC supply

Yes it is insignificant.

Hello again,

Ok great, that makes it much much simpler. If the first inductor was actually an inductor there is a chance this might be 3rd order and that could have a very complicated math structure...one that you'd only want to deal with in a computer program.

Since this is second order and the values for the components and initial values are not given, the solution is completely symbolic and there are three possible solutions based on the actual values of R,C, and the second L. These can be reduced to one equation but then we have to deal with complex numbers so i'll present this in the three different equations.

First the criterion is:
Z=4*C1*L2*R1^2-L2^2

and the three solutions depending on that result are (using more generic symbols as shown farther below):

if Z<0 then
Ft=(e^(-t/(2*C1*R1))*(((2*C1*L2*R1*((I1-I2)*L2*R1+E2*L2)-C1*E1*L2^2*R1)*sinh((t*sqrt(-L2*(4*C1*R1^2-L2)))/(2*C1*L2*R1)))/sqrt(-L2*(4*C1*R1^2-L2))+C1*E1*L2*R1*cosh((t*sqrt(-L2*(4*C1*R1^2-L2)))/(2*C1*L2*R1))))/(C1*L2*R1)

if Z>0 then
Ft=(e^(-t/(2*C1*R1))*(((2*C1*L2*R1*((I1-I2)*L2*R1+E2*L2)-C1*E1*L2^2*R1)*sin((t*sqrt(L2*(4*C1*R1^2-L2)))/(2*C1*L2*R1)))/sqrt(L2*(4*C1*R1^2-L2))+C1*E1*L2*R1*cos((t*sqrt(L2*(4*C1*R1^2-L2)))/(2*C1*L2*R1))))/(C1*L2*R1)

if Z=0 then
Ft=((t*(2*C1*L2*R1*((I1-I2)*L2*R1+E2*L2)-C1*E1*L2^2*R1))/(2*C1^2*L2^2*R1^2)+E1)*e^(-t/(2*C1*R1))

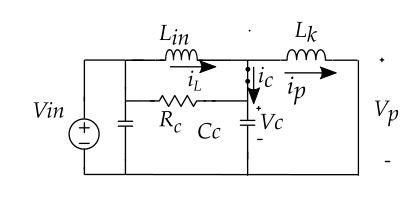
with the variables as follows:
R1=Rc
C1=Cc
L2=Lk
I2=ip
E1=Vc(0)
I1=iL
E2=Vin

I only tested the Z>0 case but you can test the others using a simulator.
Note the similarities between the Z>0 and Z<0 cases, and that Z=0 is rare.
Also note that the denominator can be factored out of the numerator in those two cases also.

 

[Archit]

Ft=(e^(-t/(2*C1*R1))*(((2*C1*L2*R1*((I1-I2)*L2*R1+E2*L2)-C1*E1*L2^2*R1)*sin((t*sqrt(L2*(4*C1*R1^2-L2)))/(2*C1*L2*R1)))/sqrt(L2*(4*C1*R1^2-L2))+C1*E1*L2*R1*cos((t*sqrt(L2*(4*C1*R1^2-L2)))/(2*C1*L2*R1))))/(C1*L2*R1)

Is Ft=Vc??
Anyway Thankyou so much....

 

[MrAl]

Is Ft=Vc??
Anyway Thankyou so much....

Hi,

OH yes, sorry. Ft=Vc(t).

Did you need the expression(s) for ip(t) also?

Here's the criterion:
Z=L^2-4*Rc^2*C*L

and here is the expression for ip(t) when Z>0:
(e^(-t/(2*Rc*C))*((
(-((i0*Rc-Vin)*C-Rc*C*iL)*L^2-2*C*L*((Rc*iL+Vin-i0*Rc)*L-Rc^2*v0*C))*
sinh((t*sqrt(L*(L-4*Rc^2*C)))/(2*Rc*C*L)))/(sqrt(L*(L-4*Rc^2*C)))+((i0*Rc-Vin)*C-Rc*C*iL)*L*
cosh((t*sqrt(L*(L-4*Rc^2*C)))/(2*Rc*C*L))))/(Rc*C*L)+(Rc*iL+Vin)/Rc

and when Z<0 change all sinh to sin and cosh to cos and change the sign under all the radicals to minus:
sqrt(-L*(L-4*Rc^2*C))

 

[Archit]

Hi,

OH yes, sorry. Ft=Vc(t).

Did you need the expression(s) for ip(t) also?

Here's the criterion:
Z=L^2-4*Rc^2*C*L

and here is the expression for ip(t) when Z>0:
(e^(-t/(2*Rc*C))*((
(-((i0*Rc-Vin)*C-Rc*C*iL)*L^2-2*C*L*((Rc*iL+Vin-i0*Rc)*L-Rc^2*v0*C))*
sinh((t*sqrt(L*(L-4*Rc^2*C)))/(2*Rc*C*L)))/(sqrt(L*(L-4*Rc^2*C)))+((i0*Rc-Vin)*C-Rc*C*iL)*L*
cosh((t*sqrt(L*(L-4*Rc^2*C)))/(2*Rc*C*L))))/(Rc*C*L)+(Rc*iL+Vin)/Rc

and when Z<0 change all sinh to sin and cosh to cos and change the sign under all the radicals to minus:
sqrt(-L*(L-4*Rc^2*C))

Thankyou once again.

 

[MrAl]

Thankyou once again.

Hi again,

You're welcome.

I should mention that the results shown are highly theoretical. To make this more practical, we should really assign series resistances to the two inductors. I say this because we have a theoretical-only situation for t going toward infinity, and that is because there is no series resistance for either inductor which could give rise to high current in an actual circuit with two actual inductors. Something to think about.
What limits the current right now (without the resistors) is the fact that we are treating the first inductor as a current source, and that current source value can not rise. In a real circuit with two real inductors, the current would eventually rise, and there would be no limit because for long time values the two inductors effectively short out the input voltage Vin.
If you want to keep the first inductor as a current source though that's fine as long as you know if the circuit is kept on for too long it will draw a huge current unless at least one of the inductors has significant ESR.

For reference, here is the set of ODE's used for the solutions:
d(Vc)/dt=iL/C+(Vin-Vc)/(Rc*C)-ip/C
d(ip)/dt=Vc/L