Does Skin Effect Increase With Voltage?

[johnyradio]

Here's a simpler, better question, than my original question .

Will these two sines experience the same percentage power loss on the same wire due to skin effect (passed separately, not at the same time) .

Vertical axis is voltage .

question as previously stated (ignore):

Assume a wire has a given skin effect depth at a particular frequency.

Compare the following scenarios:

Scenario 1: One such wire. We send a bipolar AC current at that frequency, at a particular peak to peak voltage amplitude down that wire. Due to skin effect, it will have a particular impedance, and thus a particular power loss.

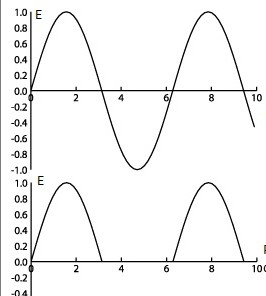
Scenario 2: Same such wire, identical to the above wire. Identical AC current. Except, we're sending the positive half ONLY down the wire. Ie, half rectified.

Will the 2nd scenario suffer the same power loss (due to skin effect) as the 1st scenario? As a percentage of the original, not as absolute amps.

Here are the two scenarios:

Or, as sine:

 

[dknguyen]

No. Because scenario 2 has half the time being 0Hz transmission, and the portion during the half-wave has different frequency (higher) components than scenario 1.

 

[johnyradio]

scenario 2 has half the time being 0Hz transmission

i don't understand what that means. I'm guessing "0Hz" means DC?

the portion during the half-wave has different frequency (higher) components than scenario 1.

If they're both square waves, won't they have the same harmonic content?
If they're both sines, won't they both have 0 overtones?

thx

 

[dknguyen]

i don't understand what that means. I'm guessing "0Hz" means DC?


If they're both square waves, won't they have the same harmonic content?
If they're both sines, won't they both have 0 overtones?

thx

0Hz = DC

Regular sine waves and half-rectified sine waves do not have the same harmonic content. The full sine wave just has one frequency component. The half rectified sine must have more. Think about what is required for it to go from flat DC into the sine-hump and back to DC again.

A fully rectified sine is also different from a regular sine wave.

Unipolar and bipolar square waves of the same zero-to-peak value sort of do but the magnitudes of the components are different (since 0Hz is different and the peak-to-peak is also different.

https://in.mathworks.com/matlabcent...s/submissions/42506/versions/1/screenshot.jpg

 

[johnyradio]

"different"
Will the 2nd scenario suffer from exactly half the power loss?

 

[dknguyen]

"different"
Will the 2nd scenario suffer from exactly half the power loss?

No. I wouldn't make generalizations like that. Look at the difference in frequency spectrums in my previous post. Different frequency components means different flow depths which makes things nonlinear. Rectification on its own is already a nonlinear operation.

https://in.mathworks.com/matlabcent...s/submissions/42506/versions/1/screenshot.jpg

 

[johnyradio]

I doubt it. Different frequencies means different depths

I think you're talking overtones, correct? Let's assume we're talking about a sine wave. Same answer?

 

[dknguyen]

Frequency components = overtones mostly, except overtones isn't truly accurate here because overtones only refers to frequencies above the fundamental but rectifying introduces a DC/0Hz component to what was initially an sine wave with a fundamental of greater than 0Hz (as well as introducing other frequency components lower than the fundamental). So it doesn't make sense to call them overtones here since things can get muddled. See the link and compare.

 

[johnyradio]

food for thought...

 

[johnyradio]

ok, le'ts assume we're talking square waves. Therefor, both scenarios are the same waveform, just different height, and one is bipolar, the other unipolar.

How might we calculate the different power loss?

thx

 

[dknguyen]

Same zero to peak value? Or same peak to peak value?
Either way, you'd have to integrate the skin losses in the wire geometry over the skin dept over the fourier spectrum of the waveform . Triple integration at least.
https://en.wikipedia.org/wiki/Skin_effect#Current_density_in_a_round_conductor

I'm too lazy to do that. I'm not even sure I could do it.

 

[johnyradio]

Same zero to peak value? Or same peak to peak value?

unclear. As described in first post.

 

[dknguyen]

Your description is unclear. Which "height" is the same between your unipolar and bipolar square wave? It's a bit moot though since the work required is the same. For a unipolar square wave peak is equal to peak-to-peak, but not so for a bipolar square wave.

 

[johnyradio]

Scenario 1 is +1V to -1V swing.
Scenarios 2 is +1V to 0V swing.

 

[johnyradio]

Can you ballpark it?

 

[dknguyen]

Can you ballpark it?

No. This is really a job for a simulator.

 

[johnyradio]

Ok, but whether sine or square, there's less loss in scenario 2, right?

 

[dknguyen]

Ok, but whether sine or square, there's less loss in scenario 2, right?

Assuming you mean regular vs half-rectified waveforms, wehther sine or square.

I don't think that's actually a fair comparison since the half-rectified wave has half the power.

But if you meant for scenario 2 to be a full-rectified waveform, then a fully rectified square wave in scenario 2 would have zero skin losses because it would just turn into DC.

I'm not sure that's true for the sine-wave because fully rectifying a sine-wave redistributes some of the energy to 0Hz which would reduce skin losses, but also introduces high frequency components that increase the skin losses. Looking at the area under the graphs I linked, it seems most of the area under the curve is pushed closer to 0Hz where there are less skin losses, but the rest of the area has been pushed to higher than the original fundamental where there are more losses so I can't really say for sure. If I had to guess I would guess the losses would be less for a sine-wave in scenario 2 as well, but that's extrapolating from the skin losses being zero in scenario 2 for a square wave.

 

[johnyradio]

Thanks much for the detailed reply.

I mean half rectified.

I added images to my OP (original post) to show exactly what I mean. Does that help?

You mentioned the half rectified wave has half the power. No matter. The question is "will scenario 2 have the same loss due to skin effect". Meaning, as a percentage of the original.

 

[unclejed613]

wow... two very similar questions about skin effect in as many days... this wouldn't be a homework question, would it?