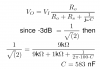Electronics4you
Member
Hi there,
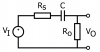
The answer to the exercise may be incorrect, since I get the wrong results every time I do the calculations. It's a simple circuit, and I need the capacitor value, so the output is -3dB at 100Hz.
I get the answer 583 nF, but the answer should be 160 nF
Can someone explain where the calculations goes wrong?
The answer to the exercise may be incorrect, since I get the wrong results every time I do the calculations. It's a simple circuit, and I need the capacitor value, so the output is -3dB at 100Hz.
I get the answer 583 nF, but the answer should be 160 nF
Can someone explain where the calculations goes wrong?
Attachments
Last edited: