Hi Fouad,
The solution is found by trying to find sections of the network diagram that can be reduced using the various rules for Block Diagrams. Sometimes it takes several steps, finding one section and reducing it and then replacing the reduced equation back into the network, then the next section, etc. This discussion will outline that procedure for one particular network.
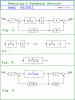
The original network is shown on Page 1, Figure 1.
We first identify the inside feedback loop, shown in Figure 2.
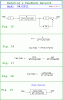
We want to reduce this sub network. To do this, we use the general formula shown in Figure 3 as "Solution". G is the forward part, H is the feedback part. Note that there are two signs for the summing junction. One sign here is positive and one is negative. The positive sign is the feedforward sign, the negative sign is the feedback sign.
The feedfoward sign is usually positive, but if it is negative we just multiply everything by -1 later (ie a gain block of -1). The feedback sign however is reflected in the variable 'm'. m takes on the values as shown in figure 3.
In Figure 4, we use that feedback solution equation to form the equation for the new gain block which we will calculate to replace the feedback loop. By substituting the values of G and H and m into the solution formula we get the result shown in the upper part of Figure 4. This gain also reduces further as shown in the lower part of Figure 4.
Now that we have the replacement gain block calculated, we replace that feedback sub network with the new gain block, and this is shown in Figure 5.
Turning now to Page 2, Figure 6 shows the reduced network as we found so far.
We next note that the new gain block can easily combine with the gain block 1/p quite easily by simple multiplication, so we do that next as shown in Figure 7.
We reduce that slightly and we see that in Figure 8.
Now that we have reduced those two blocks, we replace them with the new block as shown in Figure 9.
Turning now to Page 3, we see the network as we have computed so far. We can draw this slightly differently to make the other feedback loop more apparent, and this is shown in Figure 11. Nothing here has changed, we just redrew it slightly.
Now that we can see another feedback loop, we want to reduce that one next. Figure 12 identifies this feedback loop and the values of G, H, and m for that loop. Note we use the same formula again the only difference is the different values of G, H, and m.
In the lower part of Figure 12 we replace the variables again with their respective values. This results in a more complex equation, but we can reduce that and this is shown in Figure 13. Of course we again replace the feedback loop with the new gain block we calculated, and that is shown in Figure 14. Note how much simpler the network appears now, and that there are no more feedback loops. Thus, we've reduced the network with two feedback loops to a network that is made up of only feedforward gain blocks. That is what we wanted to do in order to get this network reduced to only one gain block eventually.
Looking at the last page now, Page 4, in Figure 15 we have the network as we calculated so far. Since there are only forward gain blocks left all we have to do now is some multiplication and addition.
We can identify that more complicated network in the center and define that as the gain 'A', as shown in the upper part of Figure 16.
In the lower part of Figure 16, all we did was multiply all the gains in the top forward path (contains the gain block 'p' but not '30') and add that to all the gains multiplied in the lower forward path (contains the gain block '30' but not 'p'). The result is shown there in the lower part of Figure 16, keeping the math form simple by using the temporary variable 'A'.
Next we simply replace both occurrences of A with its true value, and we get two terms as shown in Figure 17. These two terms of course combine and we get the final equation shown in Figure 18.
The final solution is to replace the entire network with the equivalent gain block that we just calculated, and that is shown in Figure 19.