neptune
Member
Hello folks,
I was studying Taylor's series,
Question 1: but i don't know how they got the formula for Taylor series
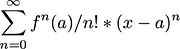
books always starts with the power series of
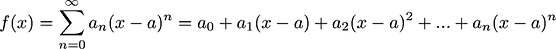
but why ?
Definition :" Taylor's theorem gives an approximation of a k-times differentiable function around a given point by a k-th order Taylor polynomial. " (source - wikipedia)
Question 2: what is k times differentiable.
I was studying Taylor's series,
Question 1: but i don't know how they got the formula for Taylor series
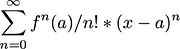
books always starts with the power series of
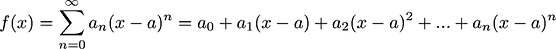
but why ?
Definition :" Taylor's theorem gives an approximation of a k-times differentiable function around a given point by a k-th order Taylor polynomial. " (source - wikipedia)
Question 2: what is k times differentiable.
