Hello there.
I started studing about reactive and active energies, and was referenced to LC circuit, where you can see how reactive energy is being transmitted and received by the power line.
I wanted to ask a few questions please:
1. I dont manage to figure out why the L's voltage looks like that, VL = L dI/dt.
What is the explanation for this?
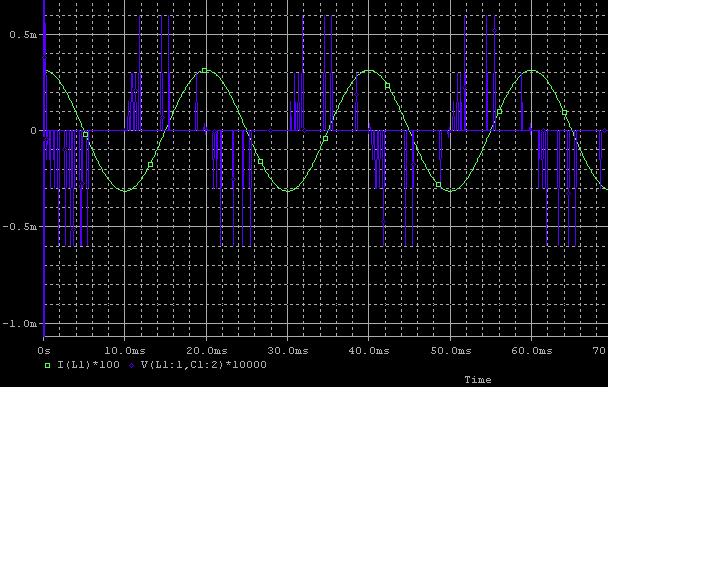
2. Why the energy of the L and C - ½LI², ½CV² - are not always possitve?
3. The energy waveform of the capacitor is much smoother than that of the inductor, which is pretty noisy.
Why is that?
Moreover, why the L's energy starts off with such large spikes that is stretched from peak to peak?
4. Is it correct to say that there are reactive energy and active energy - like in power?
Thank you very much.
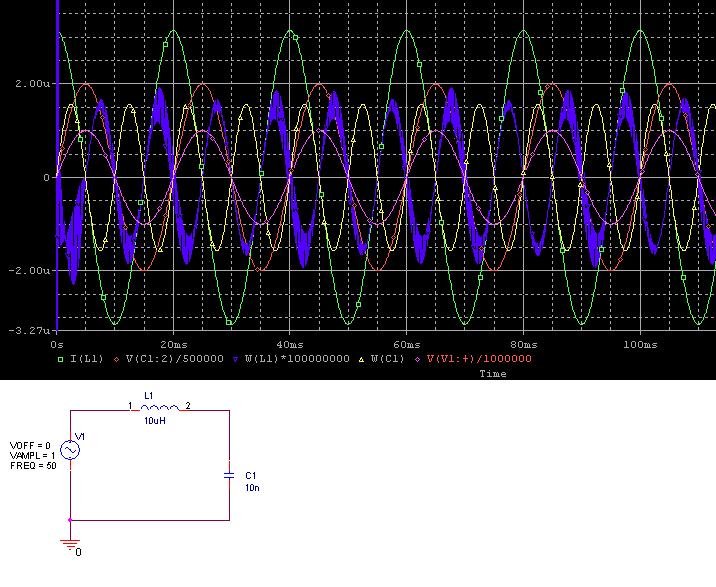
I started studing about reactive and active energies, and was referenced to LC circuit, where you can see how reactive energy is being transmitted and received by the power line.
I wanted to ask a few questions please:
1. I dont manage to figure out why the L's voltage looks like that, VL = L dI/dt.
What is the explanation for this?
2. Why the energy of the L and C - ½LI², ½CV² - are not always possitve?
3. The energy waveform of the capacitor is much smoother than that of the inductor, which is pretty noisy.
Why is that?
Moreover, why the L's energy starts off with such large spikes that is stretched from peak to peak?
4. Is it correct to say that there are reactive energy and active energy - like in power?
Thank you very much.
Attachments
Last edited:




