Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
Mr Al and PG,
What needs to be realized here is that there is a higher purpose to this exercise. It's not just a straightforward method for finding one transform, if you already have another. The method they are asking us to discover can generate the solution without need for having another solution in hand and without needing to do a complicated integral transform directly.
Notice how the simple example is given first. Solve that one, and the method will be clear. This solution is not very interesting because the answer to sin and cos are well known, in tables, or can be calculated directly from the integral transform. But, the second problem would normally be difficult. However, with this method, it is merely slightly tedious.
When solving for the transform of sin(wt), express it in terms of the transform for cos(wt), then find the transform for cos(wt) using the same method and it will be written in terms of the transform for sin(wt). Combine the equations and solve, and you will have an equation for the transform of sin(wt) directly, without need for the transform of either cosine or sine.
Hello there Steve,
Yes, and i think you are talking about frequency differentiation right? That simplifies the calculation of a time function multiplied by t one or more times. That's another useful Laplace operation.
But im not sure i understand what you said in your last paragraph. You seem to be saying that you need the transform of sin (or cos) but then in the last line you state that we dont need the transform of sin (or cos depending on the particular problem. Did you mean we calculate that one with the integral transform directly? Note that when i talked about 'knowing' a related transform before we start that doesnt exclude those which we can calculate easily.
So just to summarize then, when a time function is multiplied by time t we can use the Laplace Transform operation of Frequency Differentiation to get the more complex transform more easily. I think that's what Steve was trying to say here.
So this should work with the integral too then.
Have you tried it yet using the time integral operation rather than the derivative operation? Might introduce some complexities however but should be interesting anyway
So this should work with the integral too then.
Have you tried it yet using the time integral operation rather than the derivative operation?
Wouldn't the proof just be a double application of equation 10.5?
By the way, I recommend that you not use a star or asterisk to indicate multiplication because often this is a symbol for convolution. Instead use a small dot. If a dot is not available, then a space to separate the symbols will make it clear that multiplication is the operation between two different symbols.
I agree it looks complicated, but if you break it down step by step it can be done. I haven't worked it out, but it seems to me that you will need to apply the derivative rule many times. When you do this, you might find the function transform that you are trying to solve for, show up again in the process. If this happens, you can rearrange the equation and solve for the function transform.
Q1:
The follow is the reply to this question from post #1.
It's really very complicated and I think it would take quite an effort and labor to calculate f(t), let alone the multiple times application of derivative rule. Notice that to calculate f(t) I need to use integration by parts many times. If my fear is justified then I shouldn't proceed with this problem because I'm only doing it for my own learning. Kindly let me know. Thanks.
Q2:
I don't get the following formula. I mean what "1" stands for. Is it unit step function?
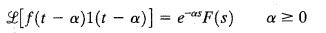
Thank you.
Regards
PG
Here are my recommended steps.
1. Find transform of sin(wt) and cos(wt) by applying the derivative rule twice
2. Find transform of t sin(wt) and t cos(wt) by applying the derivative rule as needed and using the transforms of cosine and sine
3. Find transform of t^2 sin(wt) by applying the derivative rule as needed and using the transforms of cosine, sine, t cos and t sin.
If I were to do this problem, I would proceed in a systematic way and build up useful transform formulas along the way.
Here are my recommended steps.
1. Find transform of sin(wt) and cos(wt) by applying the derivative rule twice
2. Find transform of t sin(wt) and t cos(wt) by applying the derivative rule as needed and using the transforms of cosine and sine
3. Find transform of t^2 sin(wt) by applying the derivative rule as needed and using the transforms of cosine, sine, t cos and t sin.
[latex]L\{\sin(t)\cdot {\mathrm u}(t)\}=L\{\frac{d}{dt}(-\cos(t)\cdot {\mathrm u}(t) )+\cos(t)\cdot\delta (t)\}=\frac{-s^2}{s^2+1}+1=\frac{1}{s^2+1}} [/latex]
